
the Easy Way
 |
Pencil & Paper Square Roots the Easy Way |
An Inside-Out Approach
Suggested advance reading: A Special Continued Fraction for Square Root
This method for extracting roots is unorthodox, in that it produces results in fractional form. If a decimal value is desired, then a subsequent long division would have to be performed.
The special properties of this continued fraction (CF) lend
themselves to manipulation by a calculator — or by hand:
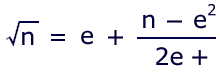
Example: for sqrt(27), an expansion of CF looks like this:
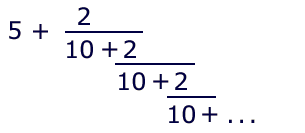
Since the original estimate never is changed, and the iterations
always use the same values, this construct lends itself to an
"inside-out" approach to the calculation —
that is, choosing an arbitrary starting point as the "bottom" of the
sequence, and working up. A sample procedure is fairly simple:
It sounds like a kitchen recipe, doesn't it? In any case, the first step is trivial; it is simply 2/10. Here is the second iteration:
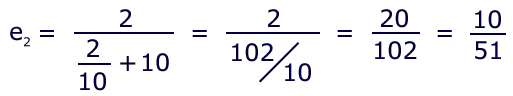
Similarly, loop #3:
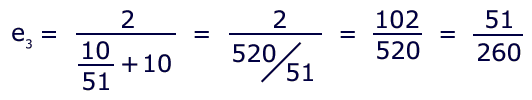
For ease of calculation, the idea is to keep the numbers as small as possible, by simplifying each fraction to two integers and by reducing to lowest terms when possible. If CF itself is in lowest terms, then no factoring will be available; otherwise, some quotients can be reduced to lower terms. In the case of 2 and 10, where both are divisible by 2, each quotient can be reduced by a factor of 2.
Warning: the original continued fraction itself must never be changed. For example, reducing a CF of 2/10 to 1/5 would effectively represent the square root of 7¼!
Here is a chart of iterations of sqrt(27):
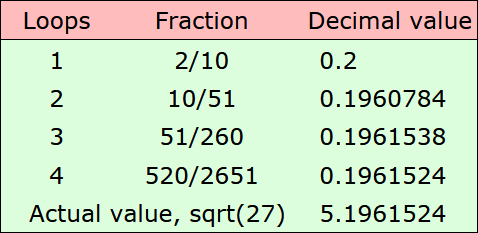
In this case, just three iterations were sufficient to achieve
5-decimal accuracy.
Now let's try a rather less friendly example — sqrt(47), using an estimate of 6:
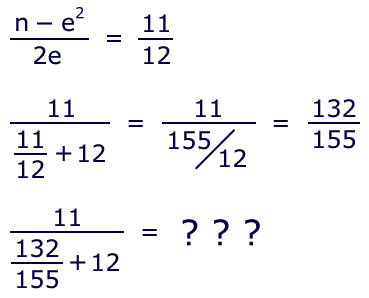
The numbers have become uncomfortably large in a hurry. At this stage, you somehow know that the prior total isn't going to be very accurate, and you are right. You probably are asking yourself why you don't just borrow someone's calculator and be done with it. The problem here is that a CF of 11/12 is too large; it converges slowly, and the size of the numerator escalates the size of all subsequent numbers.
Is there an alternative? Yes! It is not necessary that the estimate be less than the actual square root; but ideally it is as close as possible. 47 is much closer to 49 than to 36, so let's revise our setup for sqrt(47), using an estimate of 7. The CF numerator will be negative, but that's a minor detail:
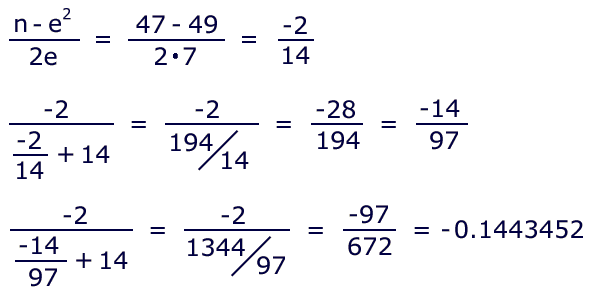
Adding the last result to 7 leaves 6.8556548,
which is sqrt(47) accurate to 6 decimal
places! Had we stopped after just two iterations, we still
would have achieved 4-decimal accuracy with minimal calculation.
Manipulating fractions in this fashion is straightforward enough; yet there is a more concise method that, with a little practice, makes the whole procedure a snap!

Plugging the numbers into this equation simplifies the process
by obviating the fractions within fractions. Calculating three
iterations should be fairly easy irrespective of the parameters.
Let's try sqrt(21) with an estimate of 4:

That's good for 3-decimal accuracy, despite a large CF: 4.5828 compared to the actual 4.5826
Note: the smaller the continued fraction, the more quickly it converges upon the root, and the easier will be any manual calculations. For maximum accuracy with the minimum of effort, it is incumbent upon you to select the closest original estimate.
Ideally, e would be the greatest integer less than the root; then the second term of the equation would calculate only the fractional, or decimal portion of the root. The working fraction also will be as small as possible. Any estimate will work, however.
So how many iterations should be performed? It depends upon
the desired digital accuracy. If the CF is relatively small,
two iterations will yield sufficient accuracy for most real-world
applications, and three iterations should satisfy anyone. If CF
is larger (over ½), then three or more iterations might be
required for meaningful results.