
for Square Root
 |
A Special Continued Fraction for Square Root |
Note: it is the following discovery and a desire to share it that prompted me to set up a website in the first place. Subsequently I have found other web pages featuring this method, but I believe that you will find this one the easiest to read.
Simple Elegance
The continued fraction is an amazing tool. Mathematical highbrows use them
for many things, such as the calcuation of the zillionth decimal of pi or another
irrational number. In this regard, square roots of positive integers are special
cases in that their fractional representations repeat after a certain "period", which
length varies depending upon the integer value. The following continued fraction
generates sqrt(19) and has a peried of six iterations:
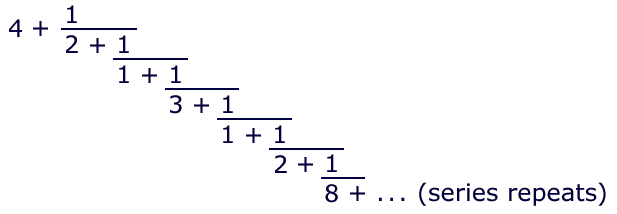
Note that all numerators in the continued fraction are equal to 1. That is the most commonly utilized configuation, yet it is not the only useful setup. Much less frequently mentioned is this fact:
• Any square root can be expressed as a continued fraction with a period of one.
The time-honored Babylonian equation provides one of those:
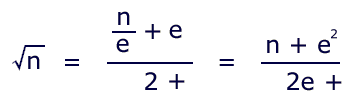
The approximation of the root is e. To calculate
sqrt(27) with an estimate of 5:
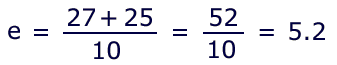
For the second iteration, 5.2 becomes the new e, and so on. The continued fraction couldn't be any simpler:
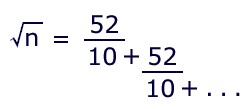
The fraction can me made even more potentially useful by an adjustment to the Babylonian equation:
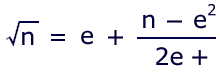
Example:
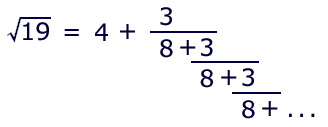
Now that is elegant!
If e is the greatest integer which square is less than
n, then the iterations approximate just the fractional, or
decimal portion of the root. In the example, 4 happens to be
the closest integer; but in fact e can be any positive value.
The following continued fractions all represent sqrt(19):
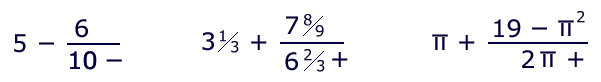
Notice that e does not have to be less than the actual root. If it is greater, then the fraction's numerators will be negative.
When e is less than sqrt(n), then successive approximations oscillate around the root, starting below it; otherwise, the series converges downward toward the root:
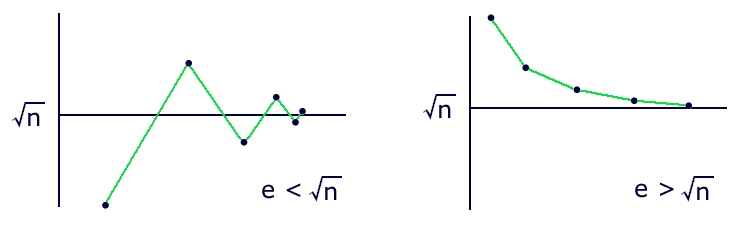
The iterations are quadratic; that is, the relative accuracy doubles with each loop.
When the digits in a continued fraction never change, calculating its value becomes a simple procedure. This fact is put to good use on these other pages: