
Tips & Tricks
 |
Mental Arithmetic Tips & Tricks |
A Few Shortcuts Are All You Need
I am a proud owner of the four-volume work, The World of
Mathematics, Simon & Schuster, 1956. The first volume
features a chapter on calculating prodigies; one was a six-year-old
boy with amazing abilities. According to the text, "When
asked for the square of 4,395, he hesitated; but on the question being
repeated he gave the correct answer, namely 19,395,025".
I decided to tackle that problem myself, coming up with a solution of 19,316,025 in approximately one minute, then was highly disappointed to see that my number did not match the one in the text. I redid the problem, arriving at the same answer as before. Imagine my elation when a calculator subsequently verified my total, showing that the book itself is in error.
This does not mean that someone should immediately sign me up
for the carnival circuit or other exposition; the problem isn't that
difficult. It does mean not only that the book's editors
were in the wrong line of work, but that if one has a reasonable
aptitude (and affection) for arithmetic, it is unnecessary to be an
idiot savant or a master of the Trachtenberg System in order to solve a
lot of everyday arithmetic problems without resorting to a pocket
calculator or (heaven forbid) pencil and paper. Although a great
multitude of gadgets is available (and well-documented online),
a small bag of tricks is sufficient for most real-world
applications.
To that end, I offer a few practical gimmicks and
shortcuts — namely, the stuff that I use myself.
Combining their powers enables one to do seemingly amazing things.
You should adopt only those methods with which you are comfortable,
and discard the rest; for an incorrect answer is worse than no answer
at all.
Note: problems are denoted as [problem]. Repeating
decimals are abbreviated by a tilde (~); so
.123123123123... is shown simply as
.123~
LEARN THE PERFECT SQUARES UP TO TWENTY OR THIRTY
If you are sufficiently aged, then in grade school you learned your
'times tables', probably up to 12 ×
12. Expanding that matrix will make your life easier.
COMMON FRACTIONS AND THEIR DECIMAL EQUIVALENTS
Rule: the decimal expansion of any fraction either ends (comes out even), or repeats a certain series forever.
That is the definition of a rational number, by the way — one that can be expressed as an integer fraction.
Everyone knows the halves and quarters:
Surely everyone also knows the fifths:
This is good. Doubtless most also know the thirds and sixths:
Slightly fewer know the odd eighths off the top of their heads:
Granted, most everyday fractions fall into one of those categories; but there are others. Ninths and elevenths are inversely related:
For a fraction such as 7/11, just multiply the numerator
by 9: (7 × 9 = 63), remembering that this
is a repeating decimal, .6363~.
Sevenths are somewhat tricky, but not difficult.
Commit this short string to memory: 142857~, and you
can master them all. Each one simply starts at a different place
in the series:
There are many other such series involving primes, but they are not
worth the mental effort. For example, there are two different
6-digit series for the expansion of n/13;
but I haven't memorized them. If thirteenths came up
a lot, I would.
ABOUT DECIMALS
Rule: decimal points control the size of numbers, but they have no impact upon the digits themselves.
That fact should be obvious to everyone, yet many solvers seem too 'locked in' to a decimal's placement to envision an easy solution to a problem.
Multiplying and dividing by 10 is trivial. You simply add
or subtract a zero, or move the decimal point one place to the right
or left as appropriate. The same applies to all powers of 10;
simply move the decimal point the requisite number of places.
That's a built-in feature of a base-10 number system,
and doubtless it already is obvious to you; but it needed to be said.
The calculating priority is to get the correct digital sequence first, then worry about where to place the dot. Because decimal points are functionally transparent to the digits themselves, they can be temporarily 'borrowed' or even ignored!
FACTORING NUMBERS
(a × b) = (2a × b/2). This conversion
can help to create friendly numbers out of unfriendly ones. Example:
[112 × 35] Working with 35 isn't easy;
but working with 7 is. So double the 35 to a
7, and halve the 112 to 56. Now the
problem reads 56 × 7, which equals 392.
Knowing that the product has to be somewhere in the range of
100 × 35, you add a zero and have your answer:
3920.
Getting rid of a fraction invariably is helpful:
[4.5 × 12.2] Double 4.5 = 9; halve 12.2 = 6.1; 9 × 6.1 = 54.9.
Other factoring can be useful. Instead of multiplying by 6, multiply by 3, then by 2. Reduce more difficult calculations to easy ones:
[263 × 16] 16 = 2×2×2×2. 263 × 2 = 526, × 2 = 1052, × 2 = 2104, × 2 = 4208.
SUBSTITUTE MULTIPLICATION AND DIVISION
Multiplying by 2 is easy. Dividing by 2 is nearly as easy. Multiplying and dividing by 5 are not quite so easy, so it might be easier to use 2's instead:
5 = 10/2. To multiply by 5, simply divide by 2, then move the decimal to the right. Example:
[3286 × 5] 3286 ÷ 2 = 1643. Add a zero, for 16,430. Done.
Inversely, 1/5 = 2/10. Example:
[14.37 ÷ 5] 14.37 × 2 = 28.74. Move the decimal one place to the left, leaving 2.874. You have the answer even before your companion has gotten his calculator out of his pocket.
This method can be expanded as far as one wishes:
n ÷ 125 = n × 8/1000, etc.
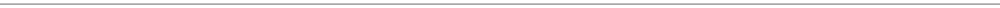
1/25 = 4/100. Multiplying and dividing by 25
are mentally difficult, but working with 4's is a different
matter. Example:
[1820 ÷ 25] = 1820 × 4/100 = 7280/100 = 72.8.
Similarly, 25 = 100/4.
[161 × 25] You observe that dividing 161 by 4 is easy enough; that's 40 with 1/4 left over, or 40.25. It remains only to move decimal right a couple of spaces; answer: 4025.
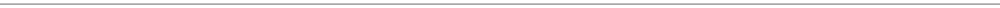
15 = 1½ × 10. Adding half of a number to itself is pretty easy, and it serves us well here.
[34 × 15] Half of 34 is
17; 34 + 17 = 51. Add a zero,
for 510. Done. Working with 15 isn't
the only possibility:
[18.5 × 45] Think 4+½.
18.5 × 4 = 37 × 2 = 74;
18.5 × ½ = 9¼;
74 + 9¼ = 83.25. Restore the
borrowed decimal place, to 832.5. Alternatively,
you could have envisioned the working digits as half/double,
or 925 × 9.
SQUARE A NUMBER ENDING IN FIVE
This ranks among the most useful of shortcuts, and it's fun! To square any number of the form (10n+5), simply multiply (n) by (n+1), then tack '25' on the end. Examples:
[252] 2 × 3 = 6; tack on 25; answer: 625.
[1.152] Ignore the decimal for a
moment. Think 11 × 12 = 132;
tack on 25, for 13225. Replace the
decimal (2 borrowed places, squared): 1.3225.
Piece of cake.
[7½2] is the same as
[7.52] 7 × 8 = 56;
append 25, for 5625; adjust the decimal,
to 56.25; convert back to a fraction: 56¼.
In this case, you didn't actually have to calculate the location of the
decimal point. You were intuitively aware that the answer could
not be as small as 5-something, nor could it be as large as
500-something. You were able to restore the decimal point
with hardly a thought.
SQUARING OTHER INTEGERS
To square an unfamiliar number, the idea is somehow to relate it to one that you do know.
Rule: The difference between (n2) and (n+1)2 is equal to (n)+(n+1).
Example: 132 + (13+14) = 142.
[362] = 352 + (35 + 36) = 1225 + 71 = 1296.
One can go backward as well as forward:
[592] = 602 - (60 + 59) = 3600 - 119 = 3481.
This method is less practical if the squares differ by more than one, but there is another way.
Rule: (x+y)2 = x2 + 2xy + y2.
We can use this:
[422] = (40 + 2)2 = 1600 + 160 + 4 = 1764.
[772] = (80 - 3)2 = 6400 - 480 + 9 = 5929. Of course, you also could have solved it this way:
[772] = (75 + 2)2 = 5625 + 300 + 4 = 5929.
Sometimes the toughest part of a problem is deciding which shortcut to use!
MULTIPLYING BY 11
Eleven is perhaps the easiest multiplier of all, excepting two. It is necessary only to sum the adjacent digits of the other number. Example:
[143 × 11] The first digit of the answer is
1; the second digit is 1+4, or 5;
the third digit is 4+3, or 7; the 3
becomes the last digit. Answer: 1573. But wait;
it's a wee bit more complicated than that.
[5861 × 11] Start from the right, in order to carry
the tens. The last digit, 1, remains the same; add
1+6 = 7; add 6+8 = 14. The working
digit is the 4, and carry the 1; next is
8+5 = 13, +1 = 14; the digit becomes a 4,
carry 1; finally comes the 5, +1 = 6.
Answer: 64,471. This method simply combines the two
steps of a standard paper multiplication.
This can be carried further:
[512 × 33] = 512 × (3 × 11); 512 × 3 = 1536; 1536 × 11 = 16,896.
PRODUCT OF TWO INTEGERS
Rule: The product of any two numbers is equal to the square of half their sum, less the square of half their difference.
This tricky-sounding identity actually is quite easy to implement, if the difference between the two numbers is even and is fairly small. Example:
[19 × 21] = 202 - 12 = 400 - 1 = 399.
"Half their sum" is merely the number 'in the middle'. In this case, the middle number is 20. Similarly, think of 'half their difference' as the difference between either number and the one in the middle. Let's try another example:
[23 × 27] The middle number is 25;
the "difference" is 25-23, or 2.
252 - 22 = 625 - 4 =
621. Child's play. If the conditions are suitably
friendly, the numbers need not be integers:
[10.5 × 13.5] =
122 - 1.52 = 144 - 2.25 =
141.75. Alternatively, you could have suppressed the
decimals: 105 × 135 =
1202 - 152 = 14400 - 225 =
14175. Then move the decimal.
A BIT MORE ABOUT FRACTIONS
We have memorized the decimal expansion of every fraction where the denominator is eleven or less, but not all fractions are so cooperative. If the denominator is prime, then there is no shortcut solution. Each prime has one or more unique repeating series, and the math gurus have been unable to establish any pattern for predicting them. However, for denominators whose prime factors are 7 or less, fractions can be fairly easily calculated. Example:
[3 ÷ 14] Mentally dividing 14 into
3 (think 30) gives us 2 with
2/14 left over. But 2/14 = 1/7,
and we already know that value. The digits must be
2 + 142857, so the answer is
0.2142857~, quick as a wink.
But not all fractions will resolve in a single step:
[77 ÷ 120] 77 ÷ 12 = 6, with a
remainder of 5. If you happen to know your
twelfths (and they are easy enough), then you are all
but finished; otherwise, perform the next step in the division.
5 ÷ 12 = 4, remainder 2. Now we
know all the digits: 6, 4, then 2/12
or 1666. Answer: 0.64166~.
Naturally, anytime a fraction can be reduced to lower terms (by dividing both numerator and denominator by the same integer), that operation always is performed first.
TESTING DIVISIBILITY WITH A DIGITAL SUM
If you attended a grade school that still supported a sensible curriculum, then you were introduced to the handy gadget of "casting out the nines" in order to validate the answer to an arithmetic problem. For our purposes, it can be useful to determine in advance whether a number is divisible by 9, by taking its digital sum. Example:
[Is 4386 divisible by 9?]
4 + 3 + 8 + 6 = 21. Unless 21 is evenly
divisible by 9, the number itself is not. This is
another built-in feature of a base-10 number system;
if we were working in base-6, we would be casting out the fives!
This method also works for testing divisibility by 3. In this example, 21 is evenly divisible by 3, so 4386 is also.
PASCAL'S TRIANGLE
This famous matrix offers quick answers to many
probability-related problems. You need only observe
that each number is the sum of the two numbers just above it.
Knowledge of that fact enables easy reconstruction of the triangle
in case you forget some of the numbers:
| 1 |
| 1 1 |
| 1 2 1 |
| 1 3 3 1 |
| 1 4 6 4 1 |
| 1 5 10 10 5 1 |
The series may be expanded as far as one wishes, but what might be done with it? Try this:
[If you flip a coin 3 times, how often will it come up
2 heads and 1 tail?]
One solution is to iterate the possible outcomes, as there aren't too many of them: HHH, HHT, HTH, HTT, THH, THT, TTH, TTT. You observe that three heads came up once, two heads three times, one head three times, and no head once. Those totals are the same numbers as are on Pascal's line reading "1 3 3 1". Such an insight would have made short work of this problem.
The triangle's values are the coefficients of binomial expansion,
(x+y)n. The algebraic representation
of our problem is:
(h+t)3 = h3 + 3h2t +
3ht2 + t3. The answer to the
problem is represented by the coefficient of the second term, the one
where the exponents are: heads=2, tails=1.
Several other exotic identities can be found in Pascal's Triangle, but I find only this most basic one to be useful for mental calculations.
COMBINATIONS
Rule: the number of different ways of selecting
(r) items from (n) items (n.C.r) is equal to:
(n × (n-1) × (n-2)...) ÷
(1 × 2 × 3...). The total number of terms
is equal to (r). Example:
[Combinations of 8 things taken 3 at a time] (8 × 7 × 6) ÷ (1 × 2 × 3) = 56. Simple.
Rule: n.C.r = n.C.(n-r). In other words,
if (r) is greater than half of (n), then subtract it from (n).
Example: (8.C.5) = (8.C.3).
This shortcut can save a lot of number-crunching:
[Combinations of 12 things taken 8 at a time]
(12.C.8) = (12.C.4) =
(12 × 11 × 10 × 9) ÷ (1 × 2 ×
3 × 4); the 12 cancels the 3 ×
4, and the 2 reduces the 10 to a 5,
leaving: 11 × 5 × 9 = 11 x 45 =
495.
These numbers also can be read directly off a sufficiently large Pascal's Triangle, but the combinations method is more easily implemented.
DATES
Being able to calculate the day of the week in one's head is very
handy; it also is quite easy, despite the fact that such problems are
standard fare at many mental-magic demonstrations (and in my
opinion, meaninglessly so). A discussion of dates is available
on this page:
[Be Your Own Perpetual
Calendar]
And that's it; the rest is up to you.
But what about that aforementioned squaring of 4395? It is
most fortunate that the number ends in 5; otherwise the
problem would have been far more difficult as a mental
calculation. My solution employs shortcuts within shortcuts:
[43952]
4395 = (10 × 439) + 5
439 × 440 = 440 × (440 - 1) =
4402 - 440
442 =
(45-1)2 = 2025 - 90 + 1 = 1936
Replace two decimals, for 193600
193600 - 440 = 193160
Tack on 25. Answer: 19,316,025.