Be Your Own Perpetual Calendar

Calculate the Day of the Week for any Date

It's easier than you might think.  A short string of digits and a short formula are all that are required for an all-encompassing calendar.  In fact, anyone reasonably proficient with numbers can perform this calculation in his/her head!  While your companions are fumbling for a notebook or reaching for a PDA, you could already have the answer.

This algorithm is well-known.  I even found mention of it in an ancient Funk & Wagnall Encyclopedia.  I merely offer suggestions for streamlining the method for ease of calculation.

The months and weekdays have serial identifications as follows:

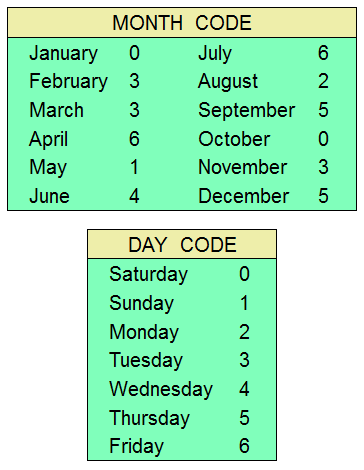
For each month, its code simply reflects the prior month's code, plus the number of days in the prior month in excess of 28.  January has 31 days, or 28+3; therefore, February's code = January's code + 3.  Whenever the number goes to 7 or higher, 7 is subtracted.  It would be necessary to memorize or reconstruct these two tables in order to do mental date calculations.

This is the magic formula:

That's all there is to it.  Here are some examples:

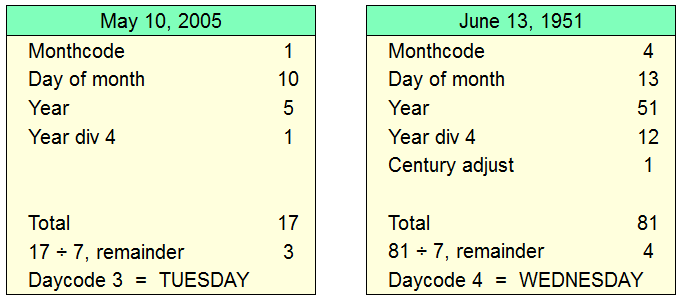
That wasn't too difficult, and we got the correct answers.  The process can be made even easier, however.  Notice that, at the end, we are interested only in the remainder; the number of 7's taken out is immaterial.  This means that we can keep our numbers small by "casting out" 7's during the calculation!  Moreover, when working in modulus 7, the value 6 is equivalent to -1, and 5 is equivalent to -2; the arithmetically adept could employ those shortcuts as well.

Let's try a more efficient approach to the second example, by removing multiples of 7 at every opportunity:

This systematic compression enables the running total to be kept to 6 or less at all times, thereby reducing the mental effort.  Of course, knowing the multiples of seven is very handy as well!

It also is helpful to file away in memory the combined code for the current year, which makes short work of any same-year calculation.  The code for 2004 is 5: 4 for the year, plus 1 for the leapyear adjustment.  So, December 31, 2004  is quickly calculated as 5 + 3 + 5 = 13 = 6 = Friday.

Happy dating!

* To go back past the last year of a century (such as 2000), add 2; to go forward into the last year of a century or beyond, subtract 2.  Change the 2 to a 1 if the end-of-century year being crossed is a leap year (that is, evenly divisible by 400) such as 2000 (yes, year 2000 was in the 20th century).  In short, add 1 for years 19xx; add 3 for years 18xx; subtract 2 for years 21xx.