Calculator Magic #7 Extra Decimals for Square Roots

Ten Digits for the Price of Seven

Prerequisite: Introduction to Programming a Four-Function Calculator
Suggested Advance Reading: Ted's Continued Fraction for Square Root

That page details an iterative manual method for extracting square roots using Ted's Continued Fraction; so I won't elaborate here, except to reiterate that this method permits one to resolve just part of the root — ideally, only the decimal portion:

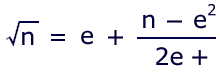
Let's investigate the square root of 19, with an estimate of 4.  The CF looks like this:

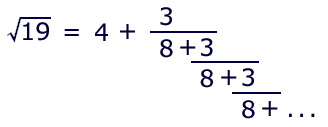
This is quickly resolved on the calculator, using our 'bottom-up' approach:

Two more iterations beget an accurate decimal portion of the root:  {.358899}.  Of course, you could simply have used the [sqrt] key in the first place — and you might as well here, because we are interested in greater things.

19 [sqrt] =  {4.3588989}

Now we add as many pairs of zeros to 19 as we can, to the limit of 8 digits: 19000000.  Each pair of zeros increases the square root of the number by a factor of 10: sqrt(19000000) = sqrt(19) × 10³= 4358.8989...

Observe that 4358 conveniently represents the greatest integer which square is less than 19000000, making it ideal for use in the next continued fraction.  Let us calculate sqrt(19000000) with an estimate of 4358.  This is the CF:

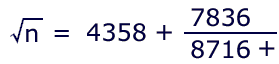
Fortunately, we don't have to remember all those numbers.  The numerator of the fraction can be handled automatically:

Three iterations are all it took, despite the size of CF.  Add that value to 4358 and move the decimal back where it started, leaving 4.3588989435, accurate to 9 decimal places!  Being able to move three digits to the left of the decimal point freed up space to calculate three more.

Let's try another one: sqrt(1234) = 35.128336

This one can be increased only by a factor of 10⁴, to 12340000.  The root increases to 3512.8336... using the same procedure as before, with an estimate of  3512:

This one required only two iterations, plus one for verification.  Add this to the estimate, move the decimal back, and we have the root: 35.128336140

HANDLING VALUES LESS THAN 1

Ted's Continued Fraction works only when n is greater than 1.  If the number is less than that, it can be increased by factors of 100 until it is greater than 1.  It makes no difference where the decimal point was located originally; the digits work the same.  Any n that can be typed into the display can be processed.

For any calculator with a typical 8-digit display, the accuracy of this method is constant at ten significant digits, irrespective of the size of the number.  Eleven digits are calculated, but the last one cannot be trusted.

One nifty feature of processing these types of iterative series is that it doesn't even matter whether a mistake is made along the way!  Any error in calculation is absorbed by subsequent iterations, although one or more additional loops would then be required in order to achieve a specified accuracy.