The Squared Square

Because there is much other online information on this topic, I have elected to share only a couple of examples.

"Squaring the square" with areas of different sizes was long claimed to be impossible.  In 1939, however, R.P. Sprague of Germany published a 55-square solution.  A major "improvement" upon that discovery was this 26-square layout, first published by W.P. Tutte of Canada in 1940:

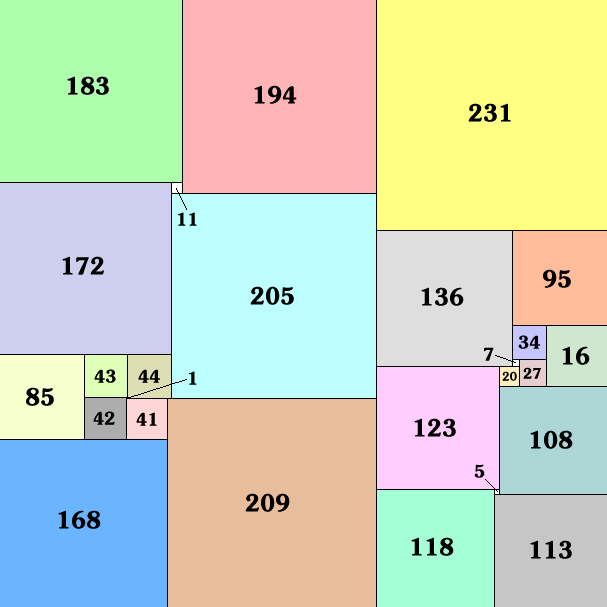
Subsequently, it has been shown that the lowest-order possible solution is 21 squares.  The matrix shown below, believed to be unique, was discovered in 1978 by W.A. Duijvestijn of The Netherlands: