Calculator Magic #8 Arithmetic Shortcuts

Summing Numbers and Fractions the Easy Way

Here are two methods for processing arithmetic terms without the calculator's memory, permitting it to be retained for another purpose.

ADDING FRACTIONS

Suppose that you would like to sum a series of fractions, such as:

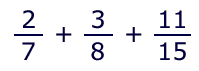
One easy solution would be to divide each fraction and put the combined results into memory:

2 ÷ 7 M+
3 ÷ 8 M+
11 ÷ 15 M+
MR

This is well and good, providing that the memory function is available.  But if it isn't:

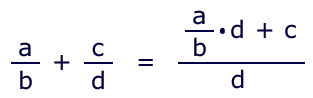
This is easily processed on the calculator without the memory.

Rule: multiply the current total by the next denominator, add (or subtract) the next numerator, then divide by the next denominator:

a ÷ b × d + c ÷ d =

It makes no difference whether the original term was a fraction.  It also makes no difference how many additional fractions are in the series or whether compound terms are involved.  Example:

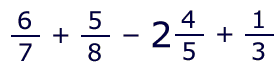
Note that negative values are merely subtracted at the appropriate time:

6 ÷ 7
× 8 + 5 ÷ 8
- 2
× 5 - 4 ÷ 5
× 3 + 1 ÷ 3 =

If that seems almost magical in its simplicity, it is!

SUMMING PRODUCTS

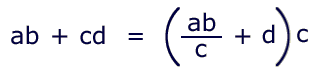
Rule: divide by one of factors in the next term, add the other, then multiply by the first one.

a × b ÷ c + d × c =

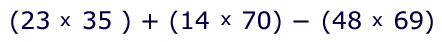
This program is equally straightforward:

23 × 35
÷ 14 + 70 × 14
÷ 48 - 69  × 48 =