
Logarithms
 |
Calculator Magic #6 Logarithms |
Increase Your Powers Exponentially
Sometimes the only way to get the job done is with a logarithm.
One example is solving for an exponent in a financial formula, such as
the term of a loan or annuity. We already know how to calculate
powers and roots of integers; logs can simplify the calculation of
non-integer exponents.
Note: A natural logarithm normally is denoted as ln x
or loge x, while the base-10 version is shown
as log x or log10 x. We are interested
only in the first type — because it's the natural thing to
do! Nevertheless, I use the term "log" in the
text for its readability, acknowledging that it is something of a
misnomer. Just think of every occurrence of the word
log as meaning loge.
Prerequisites: Introduction to Programming a Four-Function Calculator; Integer Powers
NATURAL LOGARITHMS
There are many different Taylor series representing the natural
logarithms. I have selected the one that seems to run the
fastest — that is, it produces the greatest accuracy for
a given number of program iterations:
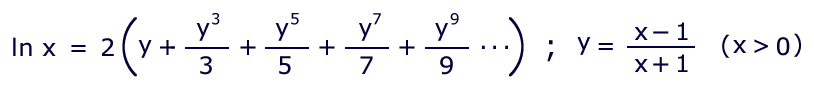
The first five terms of this series can be factored to:
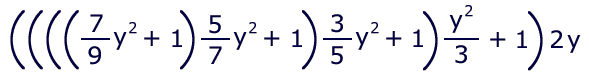
Logarithmic series converge more slowly than those for trigonometric
functions, because the fractions are greater and the series is additive.
The size of y is critical as well; smaller numbers converge faster
than larger ones. Let's try a smaller one — the natural
log of pi: log(3.14159).
2.14159 ÷ 4.14159 M+ y to memory
× = × 7 ÷ 9 + 1
× MR × MR × 5 ÷ 7 + 1
× MR × MR × 3 ÷ 5 + 1
× MR × MR ÷ 3 + 1
× MR MC × 2 = {1.1445618}
That's accurate to 3 decimal places — not bad! But this logarithm is of no value without its counterpart:
ANTILOGS
The transcendental number e has a value of 2.718281828... Its exponents are the natural antilogarithms, according to this relationship:
If log(n) = x, then ex = n. Put another way: elog(n) = n.
Not surprisingly, there is yet another Taylor series to express this function:
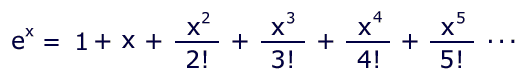
This time, let's factor six terms:
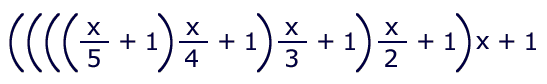
PUTTING IT TOGETHER
Rule: To take a power of a number: extract the log, multiply it by the power, then take the antilog. For a root of a number: divide the log by the exponent, then take the antilog.
As we already have the logarithm for pi, let's use that
in a problem: the cube root of pi.
In the calculator's display is {1.1445618}. From there:
÷ 3 M+ log of the cube root to memory
÷ 5 + 1
× MR ÷ 4 + 1
× MR ÷ 3 + 1
× MR ÷ 2 + 1
× MR MC + 1 = {1.4645052}
The actual cube root is 1.464592..; our answer was accurate to within one in the fourth decimal. That's pretty good, but even greater accuracy could have been achieved by expanding both of the Taylor series. Notice also how clever you were to have cleared the calculator's memory at a convenient time while extracting the logarithm; otherwise, it would have been necessary to start over.
KEEPING THE NUMBERS SMALL
This method is good only for small exponents of small numbers; otherwise, the two series resolve too slowly to produce a reasonable degree of accuracy. Without a much longer Taylor series, this method would be worthless on a problem such as 1422.5. Fortunately, there is a solution.
A non-integer exponent can be expressed as its component fraction,
enabling a solution by a two-step process. For example,
n2.3 = n23/10, or the
10th root of n23. That calculation
is readily accomplished by the methods detailed on the pages
Integer Powers and Integer Roots.
This method, however, quickly loses its appeal if the exponent is more
complicated (say 2.345), and it would be inapplicable to a
problem requiring a logarithmic solution.
As observed in prior articles, is can be easiest to factor a number
by a perfect square, if possible, in advance of taking its root.
For example, in order to calculate sqrt(80), one could
choose to factor 80 as 5 × 16, then process the
problem as sqrt(5) × sqrt(16).
Logs could be used to calculate sqrt(5), then multiply
that by the known value for sqrt(16).
2.2360678 × 4 =
{8.94427..} = sqrt(80).
A similar process enables us to treat the log-antilog process
as a sort of "black box" which ideally inputs and spits out
only small numbers — the smaller, the better.
The necessary adjustments are made outside the black box.
As the natural logarithms are based upon e, this means that
log(e) = 1, log(e2) = 2, etc.
We can use this fact to reduce the size of a number for the black box,
by dividing it by e one or more times in advance, according to
this identity:
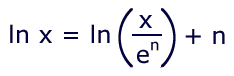
Let us put this to use, by recalculating log(pi):
3.14159 ÷ 2.7182818 = {1.1557263} = x
+1 M+ -2 ÷ MR MC M+ puts y, or (x-1)/(x+1), into memory
× = × 7 ÷ 9 + 1
× MR × MR × 5 ÷ 7 + 1
× MR × MR × 3 ÷ 5 + 1
× MR × MR ÷ 3 + 1
× MR MC × 2 = {.1447288}
+1 = {1.1447288} adds log(e)
Voila! 5-decimal accuracy, as the correct value for log(pi) is 1.1447290.. To finish the problem:
÷ 3 M+ {.3815763}
÷ 5 + 1
× MR ÷ 4 + 1
× MR ÷ 3 + 1
× MR ÷ 2 + 1
× MR MC + 1 = {1.4645868}
The 5-decimal accuracy has been maintained, which actually is more than we could reasonably expect in light of the fact that our original approximation of pi was itself accurate only to five places.
WORKING WITH LARGE EXPONENTS
It is possible to apply both base-e and base-10 accuracy-enhancers
to a problem. Let's work with some larger numbers:
1722.5
17 ÷ 2.7182818 = = {2.3006998}
At this juncture you see that another division by e would reduce the total to less than 1; this is unwanted, because it would produce a negative value for y, which doesn't work. So you stop here, noting that you took out two powers of e. Continuing:
+1 M+ -2 ÷ MR MC M+ {.3940678} y into memory
× = × 7 ÷ 9 + 1
× MR × MR × 5 ÷ 7 + 1
× MR × MR × 3 ÷ 5 + 1
× MR × MR ÷ 3 + 1
× MR MC × 2 completes the Taylor series
+ 2 = {2.8332056} = log(17)
The correct value is 2.833213, so our primitive method is
pretty close. Now we must consider the exponent. It is convenient
to move the decimal to the left, keeping the exponent greater than 1.
22.5 = 2.25 × 10; so n22.5 = n2.25
× n10. We continue the calculation, using
2.25 in the black box:
× 2.25 = {6.3747126}
That number is too big for our antilog series, so we will reduce it as well, according to this inverse of the prior identity:
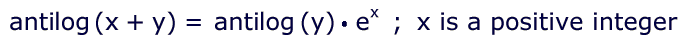
- 6 M+ {.3747126} reduce by e6
÷ 5 + 1
× MR ÷ 4 + 1
× MR ÷ 3 + 1
× MR ÷ 2 + 1
× MR MC + 1 M+ {1.4545692}
× 2.7182818 = ×(×) = = e6
× MR MC = {586.815} = 172.25
And now, the final adjustment. We borrowed 10 powers of our answer by moving the decimal in the exponent. To complete our calculation, the running total needs to be taken to the tenth power:
÷ 100 converts to n × 102
× = ×(×) = = = = {48418571} 10th power
Adding back the 20 borrowed decimals leaves:
4.84 × 1027, which is right on!
The actual value is 4.842837 × 1027.
Accuracy of three significant digits on a large exponent is excellent.