
Compound Interest
 |
Calculator Magic #5: Compound Interest |
Generating an Interest
A tutorial on business finance is beyond the scope of this article; there is just too much. I have included as examples only a couple of the more commonly used formulas.
Prerequisite: Introduction to Programming a Four-Function Calculator
COMPOUNDED AMOUNT
You plan to invest $10,000 in a 5-year CD at 6% annual interest, compounded quarterly. How much will you have at maturity? The formula is:
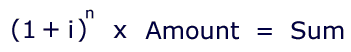
The number i is the interest rate per compounding
period — that is, the annual rate divided by the number of
compoundings per year. n is the total number of periods
(in this case, 20).
| .06 ÷ 4 M+ | quarterly rate to memory |
| +1 | |
| × = × = | 4th power |
| ×(×) = = = = | 5th power of 4th power |
| × 10000 = | {13468.54} |
Your CD will be worth $13,468.54. That was an easy one.
ORDINARY ANNUITY
You wish to set up a college fund for your child. You can spare
$100 per month to the cause. How much will you have in 18 years,
invested at 6%, compounded monthly? The formula for an annuity is:
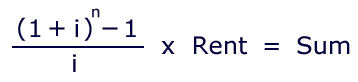
In the parlance of business math, the monthly payment is "rent", and the accumulated total is "sum". The program is fairly straightforward:
| .06 ÷ 12 M+ | monthly rate to memory |
| +1 | |
| × = × = ×(×) = = | 12th power |
| ×(×) = = ×(×) = = = = = | 18th power of 12th power |
| - 1 ÷ MR | completes the fraction |
| × 100 = | {38735.18} |
So your $21,600 in contributions became $38,735 even at a paltry 6% rate. Unfortunately, that sum won't cover your kid's expenses for four years.
AMORTIZATION
You are shopping for a home. Given the principal and the interest rate, you would like to determine the monthly payment; but you are weary of repeated calls to your broker so that he can look up the data in his little book. Now you don't have to do that. Here is the formula for an amortized loan:
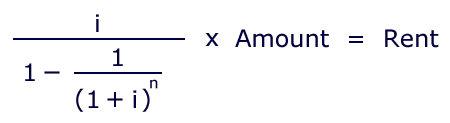
This time, the principal is called "amount", and the payment is called "rent". As before, the interest rate i will be the annual rate divided by 12 months, and n is the number of total payments.
As with the prior formula, it is necessary to process the exponential
term first in order to complete the process without the aid of pencil
and paper. To calculate the monthly payment on a loan of
$200,000 at 7%, 30 years:
| .07 ÷ 12 M+ | monthly rate to memory |
| +1 | |
| × = × = ×(×) = = | 12th power |
| ×(×) = = = = ×(×) = = = = = | 30th power of 12th power |
| ÷ 1 ÷ = | Casio: [÷ ÷ = =] |
| - 1 | Casio: [- - 1 =] |
| ÷ MR ÷ = | Casio: [÷ ÷ MR =] |
| × 200000 = | {1330.60} |
That's $1,330.60 per month, accurate to the penny!
Of course, that is just the mortgage payment. To that figure must
be added the unavoidable impounds for property tax, insurance, etc.
On a non-Casio the result will show as negative, because in
the denominator we subtracted 1 instead of subtracting from 1.
A [+/-] button on your calculator could fix that, but it hardly
matters. Somehow you know that the bank isn't paying you!
OPEN-ENDED LOAN PAYOFF
Your grandmother sold you her Victorian home for $45,000 at 8% interest, $400 per month until paid. After making 35 payments you would like to cash out that loan and clear the title, because now you can sell the place for $245,000. You would like to know the payoff amount.
The standard formula for Annuity Due doesn't serve well here,
because the term of the loan is unknown. Here is
Ted's Formula, which you won't find in any
reference manual:
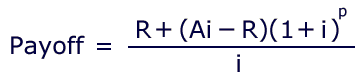
R = rent, or payment; A = amount financed,
or principal; P = number of payments already made.
This equation doesn't lend itself to single-entry calculation,
as have the others. Two steps are required; the first determines
the interest rate per payment period:
.08 ÷ 12 = {.0066666} make a note of this number. Continuing:
| + 1 | (1 + i) |
| ×(×) = = = = | 5th power |
| ×(×) = = = = = = | 7th power of 5th power |
| M+ | (1+i)p to memory |
| 45000 × .0066666 - 400 | Ai - R |
| × MR + 400 | completes the numerator |
| ÷ .0066666 = | {41067.43} |
The current payoff value is $41,067.43. Had you wished, you could have estimated that amount just by calculating the first month's interest:
.08 ÷ 12 × 45000 = {300}
So you paid $100 toward principal the first time, and slightly more in each successive month.

The four example problems were easily solved simply by knowing how to calculate a large exponent. That is not always the case, however. For example, in order to solve for i in the compound amount formula, it would be necessary to extract large roots, which we also can do. Also, solving for n, or any other exponent, requires the use of logarithms. That's the topic of the next page.