
Integer Roots
 |
Calculator Magic #3 Integer Roots |
Getting to the Root of the Matter
Prerequisite:
Introduction to Programming a Four-Function Calculator
Suggested advance reading:
Pencil and Paper Square Roots
THE NEWTON-RAPHSON FORMULA
Any root can be iteratively estimated by an appropriate formula. This one is a generalized version of the ancient Babylonian method for calculating square root. For the root of n, using estimate e:
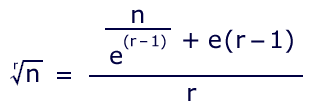
This can be restructured for easier usage on a calculator:
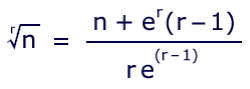
These estimates are then plugged back into themselves, yielding increasingly closer approximations of the root. Iterative methods lend themselves to easy resolution on the calculator; let's see how.
SQUARE ROOT
Although any square root can be calculated simply by pressing the [sqrt] key, this is the appropriate place to begin our enquiry. The iterative formula looks like this:
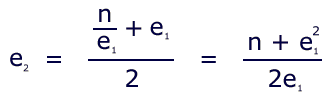
Since multiple iterations are planned, and a minimum of keystrokes is a priority, it is essential that the original estimate be entered only once, and improved estimates not at all. This is accomplished by resolving the formula from the inside out. Let's try sqrt(27) with estimate 5:
| 5 M+ | e to memory |
| × = | e2 |
| + 27 | n + e2 |
| ÷ 2 | |
| ÷ MR = |
2-decimal accuracy already has been achieved, but there is no point in stopping here. The new e is sitting in the display. You could place it in memory, and run another loop; but there is a snag: the memory already has something in it. Unless your calculator has separate MR and MC keys, you cannot clear the memory without placing its current contents in the display.
The solution is to clear the memory at an appropriate time.
A single-key addition to the program accommodates all calculators:
5 M+
× =
+ 27
÷ 2
÷ MR MC =
The memory has been cleared safely, awaiting its next usage. At this juncture, the new estimate of {5.2} is in the display. Let's run a second iteration:
M+ × = + 27 ÷ 2 ÷ MR MC = {5.1961538}
The repeated entry of n cannot be avoided, as the lone memory circuit is needed to store each updated estimate of the root.
The program can be improved even further. If another loop
is to be run, the last equal sign is redundant; when you next press
M+, the former operation is completed and the new total is
sent to memory. Also, it is faster to put the entire denominator
into memory immediately (a shortcut available only when the root is 2).
Here is a concise remake of four iterations of the program, from the
beginning:
5 M+ M+ × = + 27 ÷ MR MC
M+ M+ × = + 27 ÷ MR MC
M+ M+ × = + 27 ÷ MR MC
M+ M+ × = + 27 ÷ MR MC =
A mere 42 total keystrokes, plus n itself were sufficient
to resolve this root to 7-digit accuracy, in just a few seconds.
How about that?
The initial estimate of 5 was the closest possible, and the closer the better. Let's try another one with an estimate that isn't quite as close: sqrt(837) with estimate 20:
20 M+ M+ × = + 837 ÷ MR MC
M+ M+ × = + 837 ÷ MR MC ...
Three more loops are sufficient to resolve and verify the root to
our 6-decimal maximum! This demonstrates the awesome power
of the formula itself. Of course, had you chosen the best estimate of
29, only three loops would have been required.
It doesn't even matter whether you enter a bad number along the way. Try that last problem, then make a "mistake" by entering a 537 somewhere instead of 837; more loops will be required, but the correct root eventually will resolve.
After stressing the ease of this method, I will tell you that it could have been easier yet, by using a different formula! However, as square roots aren't the primary focus here, let us move on. They will be revisited on a later page, Extra Decimals for Square Roots.
CUBE ROOT
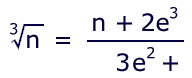
The complication of the formula has escalated due to an increase
in the exponents. Unless one is willing to record interim results
on paper (which always is an option), we need to find a way to enter a
value for e only once. It can be done. Let us
solve this problem: cube root of 73, using e = 4:
| 4 | e |
| ×(×) = M+ = | e2 to memory; e3 in display |
| × 2 + 73 | n + 2e3 |
| ÷ MR MC | divide by e2; clear memory |
| ÷ 3 = | interim estimate {4.1875} |
Remember — if the act of pressing M+ changes the display from 16 to 64, then don't enter that first equal sign on any iteration of the loop.
Unlike the algorithm for square root, the final equal sign is required at each stage. Since e2 is being stored in memory, that number needs to be recalculated first.
Let's run the second loop:
×(×) M+ = × 2 + 73 ÷ MR MC ÷ 3 =
Two more identical loops verify that the process is complete,
accurate to 6 decimal places. This stuff is easy.
It's time to move on to the next level.
LARGE ROOTS
The preceding methods were fine for smaller roots, but would be impractical for larger ones. There is no way to accommodate a single entry of e if the root is to be factored, and we don't wish to take large powers of two different numbers on every loop. A further rearrangement of the formula is in order:
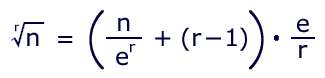
This structure converges more slowly than the other one, but it gets
the job done. Suppose that you are interested in the
72nd root of 40.
Here are the numbers:
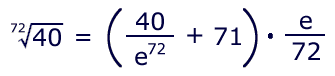
Knowing that the root will be quite small, but that it must be
greater than 1, you might simply choose an estimate of
1 for the first loop:
40 + 71 ÷ 72 M+ {1.5416666}
The new e is in memory and in the display. The next order of business is to calculate e72:
× = × = × = ×(×) = = ×(×) = = (2 × 2 × 2 × 3 × 3)
Oops! the exponent was too large for that value of e, because it overran the display. It will be necessary to start with an estimate somewhat closer to the actual root. Let's try e = 1.1:
| 1.1 M+ | |
| × = × = × = | 8th power |
| ×(×) = = ×(×) = = | 9th power of 8th power |
| ÷ 40 ÷ =(=) | Casio: [÷ ÷ 40 =] |
| + 71 × MR MC | |
| ÷ 72 M+ | {1.0853617} |
The sixth such iteration begets the correct value: {1.0525715}, accurate to 5 decimal places. Had we guessed 1.05 as the original estimate, the series would have converged in three iterations.
In this case it was convenient that r was so readily factorable, although any exponent could be accommodated.
NON-INTEGER ROOTS
Any rational non-integer exponent can be handled by considering the
root as a fraction. For example, suppose the root is
3.24. That's the same as taking
N to the power of (1/3.24), or (100/324).
So one would calculate the 100th
power of N, then take the 324th
root of the result, or vice versa. There is an easier way
to do this, however, which is detailed on the Logarithms page.