Ted's Math World - The Black Box Challenge

$Ted's Math World$

A "Black Box" Challenge

Rooting Out the Facts

Various methods for iterative calculation of square root are prodigiously documented, but I am confident that you have not seen this one previously.

You may recognize this old Babylonian formula, which approximates sqrt(n) from estimate e:

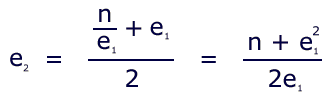
Black Box 1

The closer the original estimate, the more nearly correct will be the quotient. Successive iterations of the continued fraction yield increasingly accurate approximations of the root.

Here is my "black box" algorithm for augmenting this time-honored method:

Black Box 2

The "z-factor" greatly increases the decimal accuracy of the estimate. My challenge to you is:

How and why does this work?
What actually is happening here?

Kudos and my undying admiration to anyone who can unravel the mystery. For everyone else, details are provided. A real human would happily respond to email on this topic.

I have created a little game program to demonstrate the power of the Black Box. The player is asked to guess the square root of a random integer. The program displays the actual root, then compares it with a single-iteration estimate from the Black Box on Level-1, or with the Babylonian approximation on Level-2. The relative accuracy of a result is dependent upon the player's guess. It's a game for math nuts only.

PLAY or DOWNLOAD: ROOTS.EXE Trust me! no viruses

If you download the file, place it anywhere on your hard disk, and create a shortcut to it if you like. No other setup is required.