
"Black Box" Challenge
 |
Solution to the "Black Box" Challenge |
It's as simple as A2 B2 C2
Here is the Black Box, repeated for convenience:

The key to the solution is this Pythagorean identity:
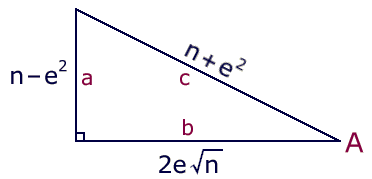
The objective is to isolate the value of sqrt(n) via trigonometric methods.
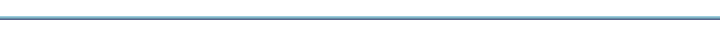
Observe firstly that:
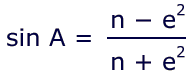
That is the x-factor, the first calculation in the Black Box.
For any angle a, if sin a = x, then arcsin x = a. There is a handy-dandy Taylor series to help us with this:
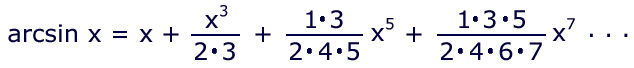
The Black Box uses the first two terms of the series: y-factor = arcsin (x-factor) = A.
The actual value of angle A is immaterial, but it is necessary to learn what it is.
Observe also from the diagram that:
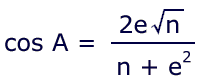
This can be rearranged to:

So it seems that the z-factor in the Black Box is equal to cos A! Interesting.
Another Taylor series is in order:
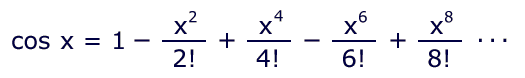
As before, just the first two terms are used as z-factor. Of course, using more terms from each Taylor Series would generate greater accuracy; but it might also have made the puzzle too easy!
A review of the Black Box:

My little game of Roots utilizes but one iteration of both the Babylonian and Black Box methods. A second loop would render any reasonable estimate far too accurate for the game's scoring to be meaningful.
The Black Box generates, on average, two extra decimals of accuracy in the first
iteration. Level-2 bypasses that adjustment, using just the older
formula.
I hope that you have been mildly inTRIGued by this study.