The Short-Suit Factor in Notrump Play

In Study #9  it was observed that possession of a 5-card suit in notrump contracts is not as effective as is commonly believed.  I contend that the principal reason for that is the fact that a 5-card suit must necessarily be accompanied by a short suit — that is, a doubleton if the hand is balanced.  Such shortness is a liability in notrump, because the extra length in the defenders' hands provides the potential for long-suit tricks.

I conjecture that best results are obtained when every suit has at least six cards between declarer and dummy.  There are just two qualifying total-card combination: 6-6-7-7 and 6-6-6-8.

Let us see whether I am right.  The following simulations of 1,000 hands each show how relatively important it is to have every suit covered with as many cards as possible.

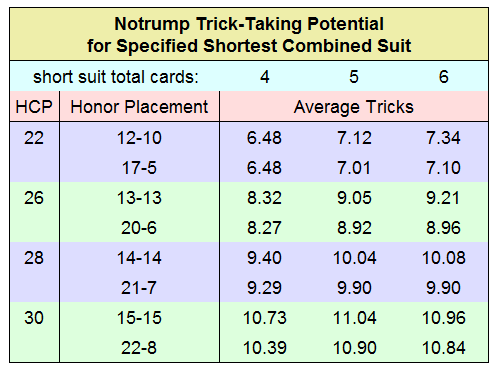
It appears that my "6-Plus Theory" is valid!  With combined holdings of up to 28 high-card points, having at least five cards in every suit produces about .6 trick or more per hand than those with opposing doubletons.  Offensive holdings with at least six cards in each suit are even more productive.

The pattern breaks down somewhat at 30 HCP, with the most balanced hands very slightly under-performing those with a short suit of five cards.  A second simulation with the same parameters produced similar results.  Your guess is as good as mine on that one.

The bottom line:

** Avoid opposing doubletons in notrump at any cost.

Don't you just hate those times when dummy comes down with a doubleton that matches the one in your hand?  And the opponents lead that suit?  Can your bidding system detect a duplication of shortness in time to avoid such a potentially disastrous higher-level notrump contract?  Is said accommodation worth the effort?

We believe that it is; for our own notrump structure specifically caters to detection of combined weakness in either major suit, and provides options for a 4-3 major contract or a bailout to four of a minor.  (There aren't enough available bids to accommodate flawed minors as well.)

The data appear to agree with us.  Six Ever, Four Never!