The Value of a Ten

The so-called Standard American point count system — devised by Milton Work in contract bridge's formative years — has proved immensely popular if only for its utter simplicity.  Although Ely Culbertson's Honor-Trick Table was considered de rigeur in the 1930s, counting all those half-tricks and quarter-tricks was tedious — and largely inaccurate.  In 1936, Charles Goren began developing and popularizing a point-count method in his own books, which instigated a 15-year battle between those titans of bridge.  Because the new 4.3.2.1 valuation scheme was much easier on the brain and more accurate as well, it ultimately supplanted the old system and remains the favorite some eight decades later.

The old Honor-Trick table overvalued kings and A-K combinations, much to the dismay of countless declarers going set in notrump contracts that should have been fulfilled according to their charts.  Conversely, today's expert consensus is that the higher honors are undervalued by the 4.3.2.1 count.  New valuations have been suggested for the ace, king, queen, and jack.  For example, one programmer's research on balanced hands suggests a rating system of 6½-4½-2½-1.  Some players add ½ point for a ten or other plus-value.  Advanced players will further upgrade or downgrade certain holdings based upon suit-lengths, honor-combinations, and spot-cards.

Experimentation with new evaluations is partially stymied, however, by the tunnel-visioned ACBL, which laws mandate that certain bidding agreements, such as the ranges for an opening One-Trump or Weak-Two-Bid, conform to Work-Points only.

In any case, I believe that sufficiently comprehensive simulations could establish a more accurate numeric ratio among the honors, by comparing their frequencies of occurrence with double-dummy trick totals over a great number of deals.  Although this seems like a straightforward analysis, I have seen no such results published as yet.  SIM will get the ball rolling here.

Today's spotlight is on the "forgotten honor" — the lowly TEN.  Oh sure — every player talks about having "good fillers" or "no spots" or the like, but the common quick-evaluation methods make no accommodation for other than the top four honors.  This oversight is a significant error, as the following data show.

For this simulation, North and South were dealt 13 hcp each.  Four different hand-pattern combinations are compared.  For added interest (and because the feature is built into SIM), each scenario arbitrarily compares the results of a contract of 1NT with a game bid of 3NT.

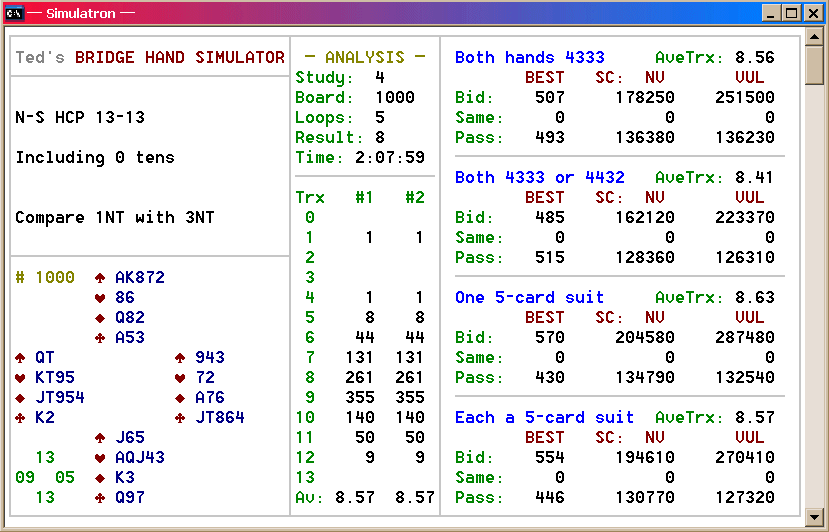
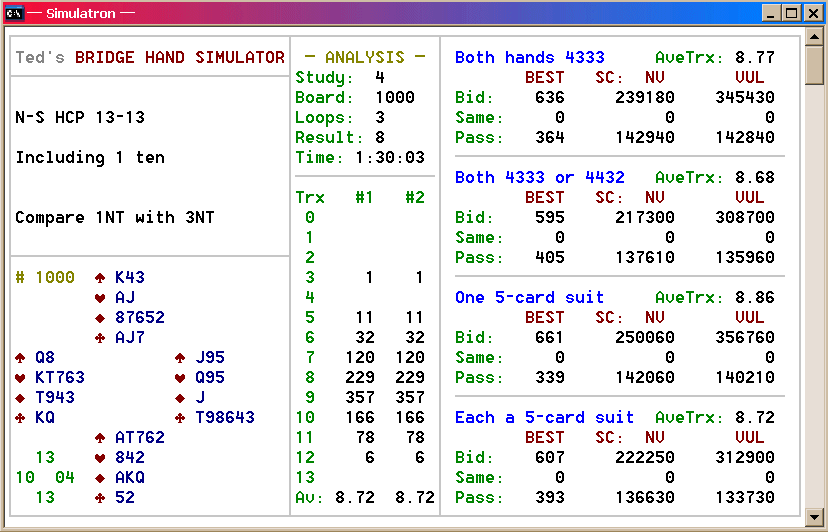
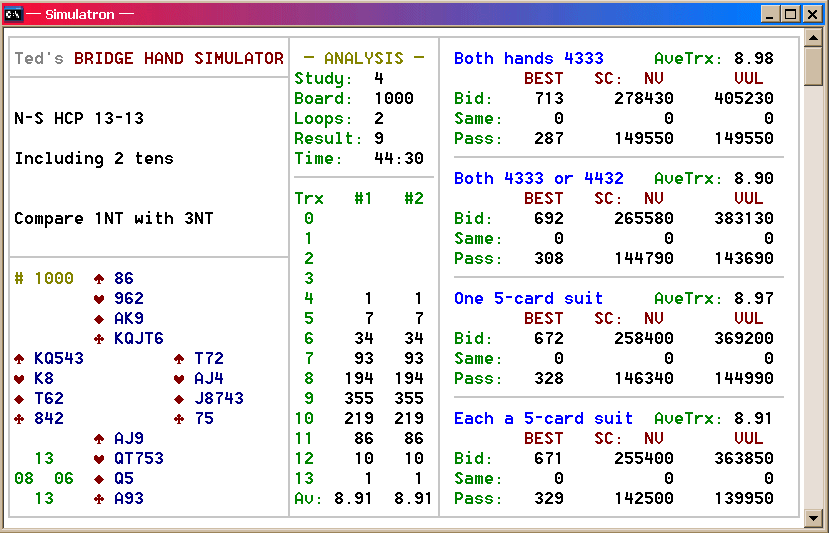
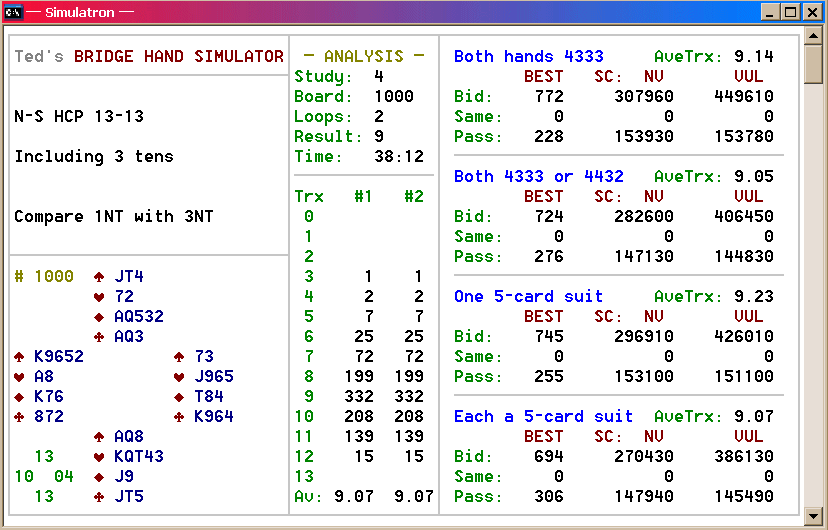
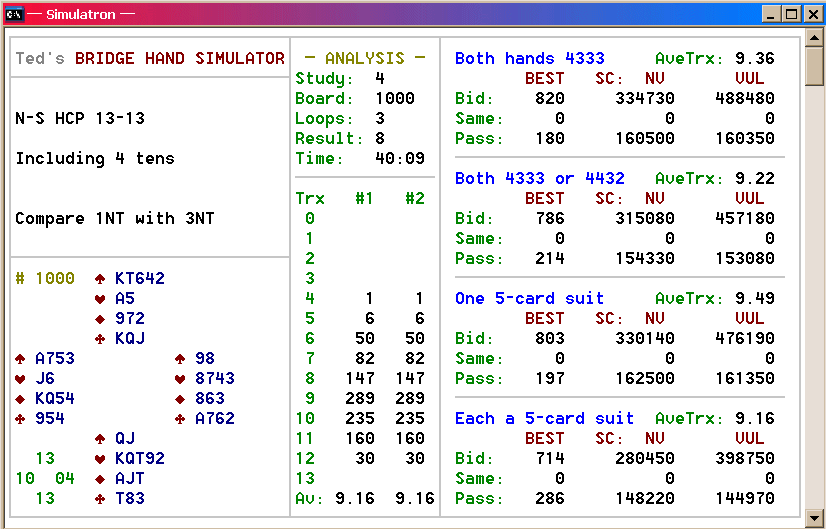
So!  It seems that the presence of tens can be worth quite a bit.

Note from the Bid/Pass data that with two 'spotless' hands, game is made barely half the time despite the 26-hcp total; yet nearly 80% of the ten-rich games succeed.

Let's compress the trick data for readability:

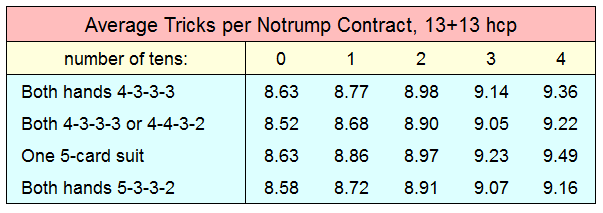
Fascinating!  Although the actual increments between boxes vary somewhat due to the relatively small sampling of these studies (1,000 deals each), the tendencies are clear: possession of supporting ten-spots is a big deal.

The difference between having no ten and possessing them all is approximately .6 to .8 tricks, which translates roughly to one-sixth of a trick per card.  On average, the offensive side will possess nearly half of the ten-spots anyway; but when all are working together, that's an additional trick on every third hand that you play.  Those tricks score up a lot of extra game and slam bonuses.

In terms of total points, the numbers are equally astounding.  This chart condenses the total-point expectations, assuming that game is bid on every hand:

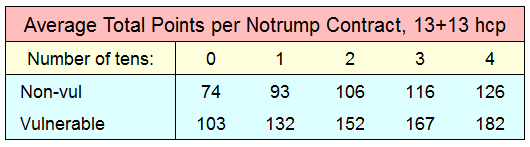
Wow!  It seems that a ten is worth approximately 13 points non-vulnerable, and about 20 points when vulnerable.  The ten-rich hands generate fully 70-80% more total points than their substance-bereft counterparts!  Compared to the average holding of a pair of tens, having all four is worth about 20% additional total points.

The bottom line: Within our test framework of balanced hands with 13 × 13 hcp,

** Each ten is worth roughly 1/6 of a trick.

** Each ten adds an average of 10-15% to the final score!

Translating a ten's worth into a meaningful equivalent high-card-point value is more difficult, but eventually SIM will determine The Way It Is.  The merits of lesser spot-cards might be examined as well.

Note from the graphs that the hands with opposing 4-3-3-3 patterns fared better than when 4-4-3-2 patterns were included.  Why?  Also, declarers with but a single 5-card suit to work with handily out-scored those in which both hands had a 5-card suit.  Why?  That seems non-intuitive, and the literature offers little if any insight into this phenomenon.  I believe, however, that SIM already has suggested the answer — to be detailed in an upcoming study.