

 |
 |
Responding to a 15-17 Notrump – Part 1
3.2.4.4 Pattern, 8 HCP
Do you invite game with a balanced 8 hcp? What if you have a
5-card minor? How good must it be? What about a
6-card minor?
Such questions arise frequently; they need to be answered.
SIM's discoveries just might cause you to revise
your thinking as to what constitutes a game-invitation or acceptance.
Most players are adamant about passing a 1NT opening
with a nondescript 8-count that does not include a major.
Let's see whether they are right. Here is a
SIM screen-dump of a random sampling:
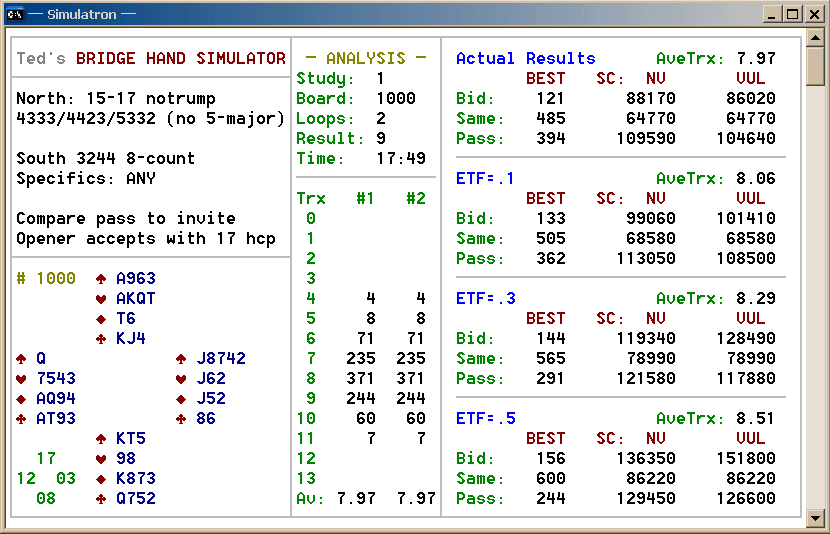
The upper left-hand box shows the study specs. The deal shown
is the last one randomly dealt (including a table of high-card points
for each hand).
In the center is the double-dummy output; the lower section is a count
of the various numbers of tricks taken by declarer (in this case North),
plus the average number of tricks won. Trick totals are broken down as
Part 1 — the pass of 1NT,
and Part 2 — the result of inviting game.
In this particular study the totals match, because the final contracts always
are the same denomination (notrump).
Note that the plurality result was eight tricks, which somehow doesn't surprise us at all.
The statistics on the right-hand side are broken down by the
Extra-Trick Factor (ETF).
Perhaps the most useful value of all is the trick-expectation,
or Average Trick Rating (ATR) for a given study.
BEST is a direct comparison of scores for matchpoint purposes only: invite vs. pass.
* Passing 1-notrump is the standout choice at matchpoints.
The other columns show the total points earned (duplicate scoring always).
NV = non-vulnerable;
VUL = vulnerable.
Note that if your side is vulnerable and your ETF
is high, bidding is best in the long run, as 10-20% more total points
would be earned that way.
* Inviting game is best at imps with a high ETF.

There is more to this story, however. In Study #1,
opener accepts only with a 17-count. What would happen if one
were to accept with any non-minimum — that is, 16+ hcp?
Here are the results:
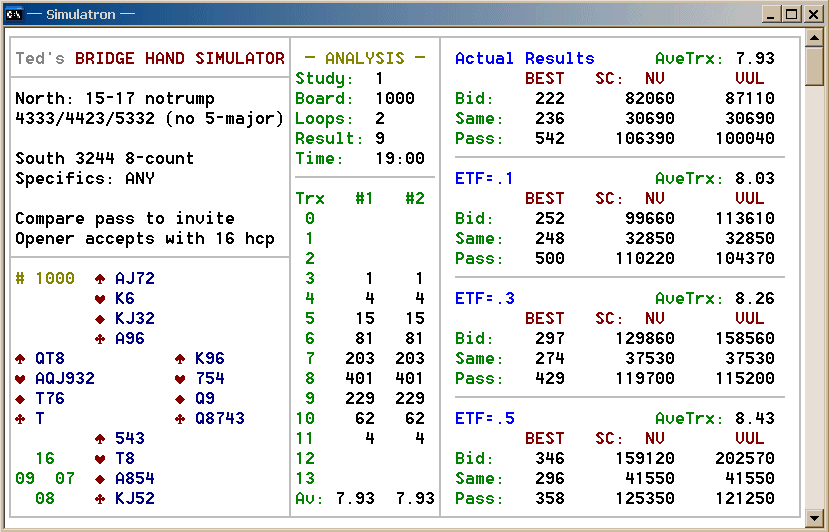
Little has changed in the matchpoint column — passing remains a
prohibitive favorite. But look at the vulnerable totals if you declare
better than your opponents defend. With an ETF of .5, accepting
game with any non-minimum scores nearly 67% additional
points overall! That's 80 extra points per hand, day in and
day out. Are they worth having? You betcha! Even an
ETF of .3 scores an average of 43 extra points per hand.
* At imps, unless your opponents are as good as you,
accept with 16-17 hcp!

We're on a roll, so let's not stop here. What if responder
were simply to raise 1NT to game every time? Let's
find out:
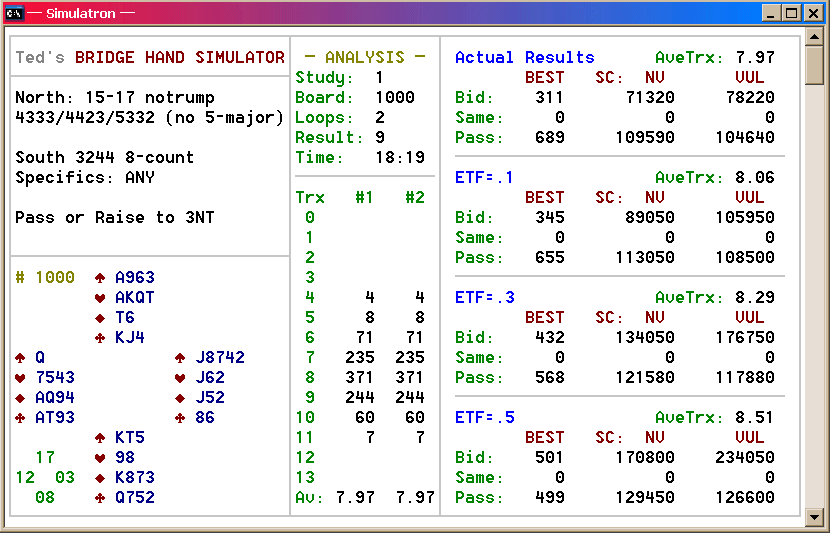
Okay — perhaps we went overboard here; most numbers are down. But we had to know.

NOTE: Our simulation is somewhat flawed in that it dealt the
E-W hands totally at random, not taking into account potential
interference. Also, the specifications denied opener a 5-card
major or any 5-4-2-2 or 6-3-2-2 pattern. Including those
options would change the output specs somewhat.
As SIM's development progresses, I will
re-run this study to accommodate these issues. I submit that the
new results will make game invitations more favorable than before.
The Best and Worst 3.2.4.4 Hands
Having assimilated all of the above, you have tentatively decided to
compromise. Your will raise partner's opening 1NT
bid only with the best 8-point hands; but which ones are those?
Before reading on, consider the following hands. Which ones do you think best support a strong 1NT opener?

In the following charts, the last column displays the hand's
Average Tricks Rating (ATR). That is the number of
tricks that each hand type would produce opposite random balanced hands with
15-17 hcp. Since the ratings can vary by as much as 0.1
(approximately 1%) depending upon the specific sample set, the second
decimal value is not particularly meaningful; I included it just to "break
ties."
The ATR for all hands is 7.97. This means
that getting even as high as 2NT is risky because, against
perfect defense, the contract would fail more often than not.
Some hands fare better than others, of course; let's compare various
honor-configurations to see how they measure up to the average.
Here are those with the lowest ratings:

Hand #1 wins the booby prize. It is the worst
8-point hand of its pattern that one could pick up.
Notice that having most of the honors in the longer suits is not necessarily
advantageous when partner's cards are randomly dispersed.
* Avoid 'quacky' hands; they just don't get the job done.
The next group is somewhat better:
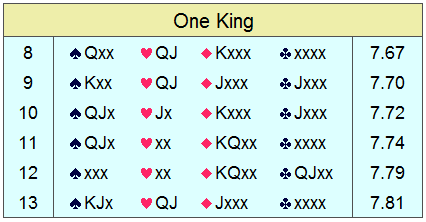
Q-J doubleton is not as good as one might have guessed, as support for partner's heart holding.
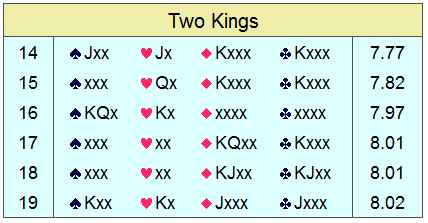
Notice how much better #19 fares than #14, with its kings swapped
to the short suits and the jacks to the long suits. Some would find
that non-intuitive.
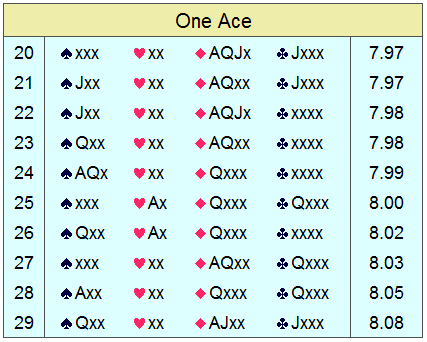
Aces are good! In case there was any doubt that they are undervalued
in the Work 4.3.2.1 point-count, this study helps
to confirm it — at least with regard to notrump play.
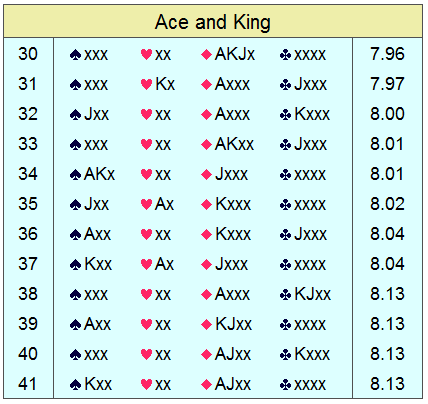
* Having all one's stuff in a single suit is not best.
Even though those aces can win only one trick apiece, their control
values easily outweigh most other card combinations, including such hands as
#2 and #3, each of which contains six honor cards.

Notice these similarities:
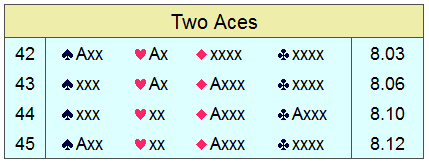
Since the top four hands tied in the overall ranking, I ran a longer
simulation just for the fun of it — 3,000 deals
each — featuring just those four patterns:
In this expanded run, the Average Trick Ratings differ by up to 1%, which is not at all unusual.

Although these are not all the possible configurations of 8 high-card
points, I believe that we have learned what works best:
* Consider a raise only when holding an Ace and King, or two Aces.
* AJxx and KJxx are the best 4-card suits.
* Avoid having an honor in the doubleton suit.
A final note: Remember that the card combinations that worked best would
not necessarily be best if south's distribution was any iteration of
4-4-3-2 other than specifically 3-2-4-4. The numbers are
skewed slightly by the constraint against north's having a 5-card
major. A perfectly fair comparison would eliminate such a factor.
Nevertheless, as most pairs do apply this bias to their own bidding styles,
the data are applicable to their methods.
The bottom line:
** There is no hand (absent a major) that merits a raise at matchpoints.
But:
** Any of the better hands is worth a raise at imps if your ETF is high.