

 |
 |
The Magic of Mirror Hands
Double-dummy aficionados should revel in these studies. Although research on symmetrical hand-types has been done by others, little has been published about this amazing feature of the world of card play.
It is time for a comprehensive analysis in this area. To that end, my
computer has generated and analyzed every possible mirror hand of every
distribution — a process requiring a lot of programming and CPU
time. In light of that, I feel that I can speak accurately when making any
definitive statement such as "that is not possible", or "no such
hand exists".
I use the term "mirror" not to suggest an actual reflection, but
to denote positional equality for all players. Mirror deals are those
configured in such a way that the four hands are strategically identical;
that is, from all four sides of the table, the layout plays the same.
Every hand has the same pattern, such as some 4-4-3-2 or some
6-4-2-1. It necessarily follows that each suit is divided in the
same ratio as the hands; that is, if the hand patterns are 5-4-3-1,
then all suits divide 5-4-3-1 as well.
The specific orientation of the suit segments also is the same in each case.
For example, if North-South have a 6-2 fit with that suit splitting
4-1 offside, then that same condition exists for every hand around the
table. By default, each hand contains exactly one card of every
denomination — that is, one ace, one king ... one deuce. Were that
not the case, then the hands would not be equal in power.
The result of this parallelism is such that if, for example, south can win 9
tricks in a certain trump suit, then each of the other hands also could fulfill
a 3-level contract in one of the other suits. There are many thousands
of such deals; the most obvious (and most trivial) case is the one in which each hand
is dealt a 13-card suit, and every declarer can win all the tricks with his own
suit as trumps. More interesting, however, are the lower-level deals
such as those on which any declarer can make 1-Notrump. Conversely,
there are many patterns wherein no player can make any contract at all!
We will look at some of the more exciting variations of each type. In all cases, analysis of the play is limited to contracts declared by South, since other consideration would be redundant. Some analytical details will be specified; some will be left to you. Let's begin with my favorite group:
— NO PLAYER CAN MAKE ANYTHING —
Not surprisingly, the uppercut is a key feature in many of these layouts. Here is a straightforward example:
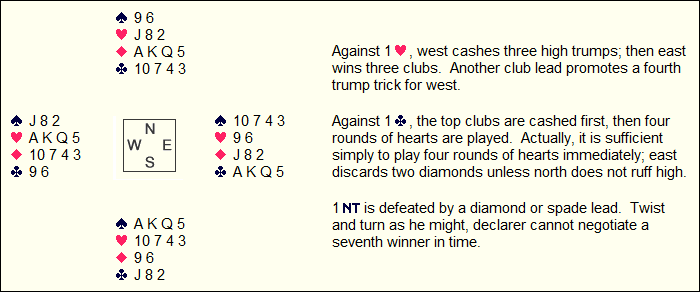
Grabbing tricks early is critical in most non-making layouts. Also, key sluffs can deprive declarer of the necessary communications between the two hands:
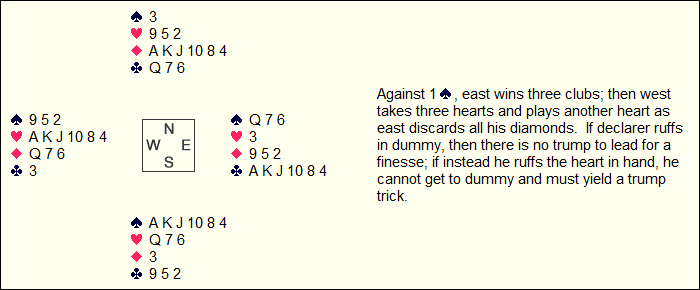
An early crossruff is the order of business here:
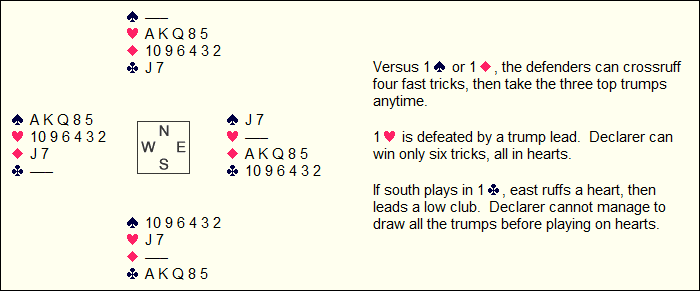
This tricky layout involves a key finesse, judicious sluffs, and perfect timing, as the defenders mold the north and east hands into a pattern of their choosing:

Sometimes an uppercut can occur as a sort of delayed reaction:
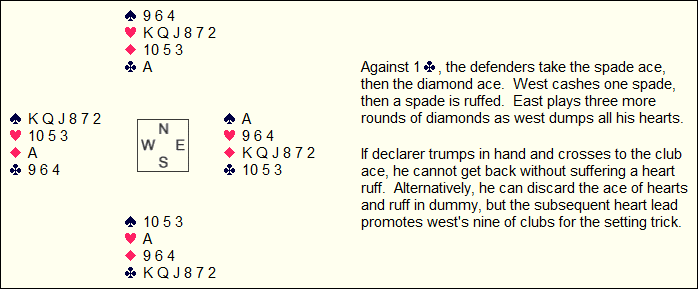
Sometimes only the defenders have communications between their hands. This one is such a case:
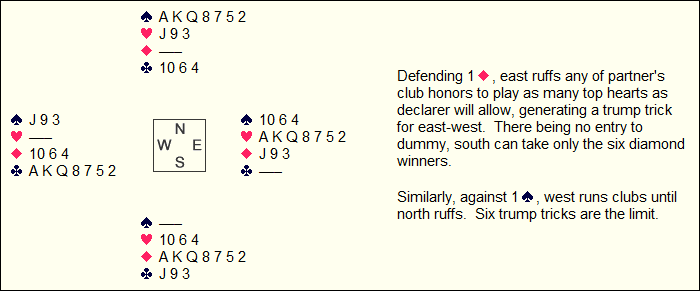
The whole game here is to prevent declarer from scoring more than five trump tricks plus his only cashable plain-suit winner:
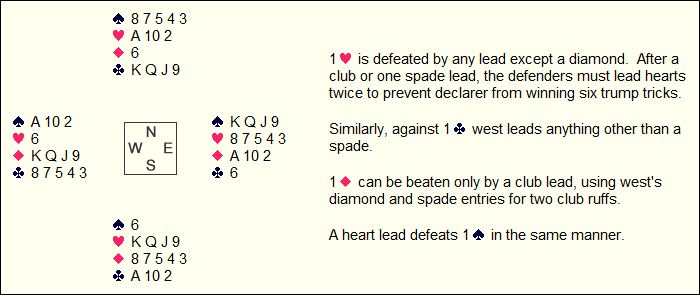
Here declarer finds himself whipsawed in the trump suit:
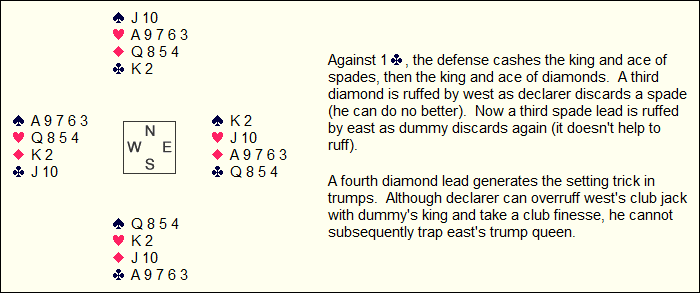
Finally, a simple suit-blockage often ruins declarer's day:
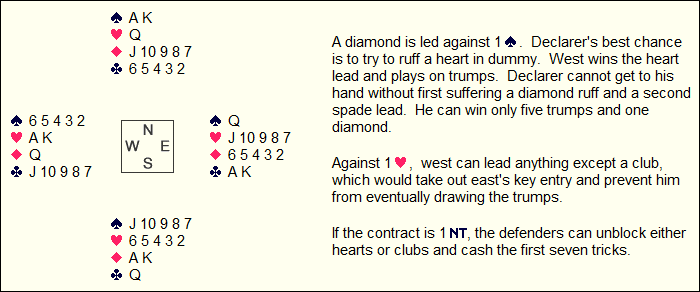
On some hands the placement of the spot-cards is absolute; that is, no two
cards could be exchanged without destroying the delicate matrix. We will
look at one of those later. On other deals there are varying degrees of
flexibility. For example, on the 4-4-3-2 deal above, all the deuces
and treys could be exchanged, or the fives and sixes, or the sevens and
eights — but only because they would be swapped across the table and
are of strategically equal value in this layout. It would remain the case
that no declarer could make any contract.
In contrast, all spot-cards in the 7-3-3-0 hand are immaterial; also, the tens
and jacks could be exchanged. There actually are 20,160 different ways
in which this layout could be arranged in mirrored fashion without strategic change.