Calculating Contract Odds by Ted Muller

Assessing the relative merits of a bridge contract entails two types of calculations:

1. Combining known odds into an overall percentage chance.
2. Analyzing both the trick-taking potential of a specific suit holding and the best way to play that suit.

There was an example of each query in tonight's session:

#1:  As west, you played the following hand in 4♥:

Your contract failed.  In the postmortem, you wondered just what your chances really were.  With a normal 3-2 trump split, either a winning diamond finesse or 3-3 spades would have seen you home.  Had the trumps proved to lie 4-1, then you would pretty much have needed both diamonds and spades in your favor.  What was the overall likelihood of success?

#2:  Still sitting west, you declared this board in 3NT against a normal spade lead:

Your contract hinged upon bringing in four diamond tricks. What was the chance of that?  Was your partner justified in inviting game?

Perhaps that second round of margaritas was to blame, but no one in your group offered an answer to either question.  Not all was lost, however; grabbing a pencil and your companion's soggy napkin, you quickly dispatched the solutions to the amazement of all.  How were you able to manage it?  Were those geometric scribbles of yours some sort of magical incantation?  No, you had merely utilized a visual aid in your algebraic quest.

Such is the potential value of graphical concepts such as Venn Diagrams, which long have served as representations of logic problems and their solutions.  For our investigation, however, we will venture into the discipline of logic only insofar as it is applicable to analysis of bridge hands.

In beginning, I will beg the indulgence of any reader skilled in math or logic, who doesn't require all the instructional details provided.  Bear with me.

This enquiry will not teach you how to calculate such things as the likelihood that a suit will split 2-2; those sorts of numbers are derived from a complicated formula involving factorials and permutations, so they are not the stuff of late-hour computations at the pub.  In any case, such figures are readily available from tables in the Encyclopedia of Bridge and elsewhere.

Note:  those a priori values are totally accurate only in the context of all possible distributions.  In real life, the odds are skewed by factors gleaned from the bidding and discovered in the play.  For example, is the 3-3 heart split really a 36% chance?  Answer: it depends.  If your left-hand opponent has eight red cards to your right-hand opponent's four, then the odds are roughly 9 to 5 that RHO has any particular card in a black suit (there being that ratio of room in the hand for non-red cards).  This skews the chances of an even division of the hearts.  The stated 9-to-5 ratio is inexact as well; the actual odds involve those aforementioned formulas as applied to the permutations of each opponent's non-spades.  For our purposes, however, the published figures are plenty close enough, and we shall treat them as such.  What's a percentage point or two among friends?

What we can do is to determine a guideline for combining already known values, as specified by an appropriate (logic) statement describing the conditions for success of a contract.  Translating logical relationships into mathematical terms is what this section is all about.  Every logical statement has an algebraic equivalent.  Three such relationships are essential to our study.

P  -and-  Q

Everyone knows that the chance of winning a finesse is 50%; all other things being equal, that pesky honor is equally likely to lie on either side of the table.  Most also know that the likelihood of winning a pair of finesses is 25%; but where did they get that figure?  Well, somewhere it was learned that when two events are mutually dependent, the likelihood of both occurring is equal to the arithmetic product of the individual chances.  In this case, .50 × .50 = .25.  In the language of logic, this event is termed, "spade finesse  -and-  diamond finesse".  The logical "and"  function proposes that "both are true", or in this case that both finesses will win.

Rule #1:  The logical  (A and B)  translates algebraically to  (a × b).  In simpler terms:  P(A and B) = ab.

This relationship can be illustrated by a Venn Diagram:

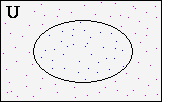
But first, a mini-tutorial.  The area inside the box represents the Universe, or all possible outcomes of an experiment; nothing outside the box has any relevance.  The area within the oval represents outcomes that meet specified criteria.  Outside the oval is all the trials that 'failed' the experiment.  Think of these areas as being filled with small 'dots', as shown, each of which represents one element, or one possible outcome.

For example, the Universe might be comprised of all possible distributions of the opponents' hands, and the oval area would include those layouts in which the queen of trumps is singleton.  But such a one-variable picture is of instructional value only.  More useful is the next diagram, which depicts two events:

Let's conduct a hypothetical experiment, using numbers familiar to us.  In this case, our Universe is a standard pack of 52 cards.  We will shuffle the deck, then draw a random card.  In the diagram, the left-hand circle represents all the clubs, and the right-hand circle includes all the honor cards.  Intuitively, the yellow area, or "intersection" of the areas, 'contains' those cards that match both criteria.  Outside the circles lie all the remaining cards.

What is the probability of drawing a club honor?  One way to determine that would be simply to count the elements in the yellow section, if possible, and divide by the known Universe of 52.  But what is the value of this intersection?  Viewing the diagram in a new perspective:

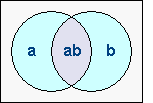Since the purple area represents the elements wherein both a and b are true, we know from Rule #1 that that area is numerically defined simply as ab!  As there are 13 clubs and 20 honors in the deck,  P(club) = 13/52, and P(honor) = 20/52; therefore, P(club -and- honor) = 13/52 × 20/52, or 5/52.  Surely enough, there are 5 club honors.

Let's try another one.  If you need three things to go your way, the procedure is similar.  You simply take the product of the individual probabilities.  Needing a 2-2 trump split, a finesse, and a 4-3 division in a side suit, you would multiply .40 × .50 × .62 = .124, or about 12%.  The logical statement here is: "2-2 split  -and-  finesse  -and-  4-3 split".

It makes no difference how many events are involved, as long as they are mutually dependent — that is, all must occur.

Rule #1  can be expanded to:  P(A and B and C ... and Z)  =  (a × b × c ... × z)

This formula conforms to the Associative Law — an axiom of mathematics, meaning that when using the -and- function, a statement's elements may be combined in any pattern or sequence.  For example:  (P and Q) and R  is equivalent to  P and (R and Q).  Intuitively, you already knew that — it makes no difference in what order you multiply a series of numbers.

P  -or-  Q

On the next board, a preempt by your opponents caused you somehow to miss your 9-card spade fit; so you find yourself declaring in diamonds.  Your contract will succeed if either trumps split 3-2 or the spades divide 2-2.  How does one calculate that?

In logic (as in English) the operative "or" is inclusive; that is, it means "either or both".  When you speak of "diamond finesse or spade split", that includes the possibility of both things working.  Numerically, it means "at least one is true".  Now I will tell you that the chance of  "probability−A  -or-  probability−B"  is equal to their sum, less their product.

Rule #2:  The logical  (A or B)  translates to:  (a+b−ab)

For visual clarification of this, let's try a different experiment with our shuffled pack.  What is the chance of drawing a club or an honor?  13 clubs plus 20 honors = 33 total cards.  Is that the correct answer?  No, because the club honors have been counted twice!  As seen in the diagram, counting the dots in each circle and combining the totals results in a double-count of the yellow area.

Let us label the pink circle (clubs) as c, and the green circle (honors) as h.  The graphing of (club -or- honor) includes the combined areas of the two circles.  As the yellow section has a previously determined value of ch, the double-counting of the club honors can be corrected by subtracting that value.   (c+h−ch) = (13/52 + 20/52 − 5/52) = 28/52, the correct answer.

Returning to our misbegotten diamond contract, we need a trump split (68%) or a 2-2 spade division (40%).  Placing actual percentages into a diagram can provide a useful picture of the situation:

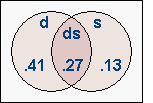The centermost area  ds  is calculated first: .68 × .40 = .27.  Section  d  then becomes  .68 − ds , and section  s = .40 − ds. Adding  .41 + .27 + .13, we come up with 81%, the likelihood of fulfilling our contract.  (Just for the record, the actual value for a 2-2 split is 40.6% — closer to 41%; but it is so much easier to use the round number!  Do what you feel is best.)

Upon further analysis, you realize that an onside club ace also offers the potential for an extra trick, and that's a 50-50 proposition.  Now our contract requirement becomes: trump split -or- spade split -or- club finesse.  It so happens that the Associative Law also is applicable to this construct; therefore, it can be stated as  (D or S) or C, or as S or (C or D), or any possible arrangement.  Let's try the first one:  (.68 or .40)= .81.  Then, (.81 or .50) = .90, or about a 90% chance overall.  Had you opted for the second pattern, you would have calculated  .40 or (.68 or .5), for the same result (within 1%, due to possible rounding errors).

Rule #2 Expanded: The logical  (P or Q or R)  can be restated as  ((P or Q) or R), or any other choice of variable sequencing.

There is a nifty shortcut for making this calculation, using the logical -not- function; however, as is it technically not required for our purposes, I have placed it at the end of this section, just for the dedicated analyst.  See the Addendum.

Mixing  -and-  with  -or-

This time you have a 5-3 heart fit; but the long trump suit is tapped at trick two.  There is other work to do; so you cannot survive a poor trump split.  Assuming that hearts divide 3-2, your game is a make if you can win the diamond finesse or split the spades 3-3.  How good is this contract?

The logical statement here is  (heart split  -and-  (diamond finesse  -or-  spade split)).  The trump split being an absolute requirement of success, that factor is not stated as part of a contingency such as (trump split or other).  It must be a stand-alone term of an -and- statement.

In any algebraic equation such as  a(b+c), the processing hierarchy is "inside out"; that is, expressions inside parentheses are evaluated first.  B and C are added, then the sum is multiplied by A.  Subsidiary to that, any multiplication and division are processed before addition or subtraction.  The same sort of hierarchy applies in the world of logic.  It is essential to format your statement accurately — that is, to "say exactly what you mean."

Our equation, (H and (D or S)), translates to  h(d+s−ds) = .68 × (.5 + .36 − .5 × .36) = 46%.

P  -or else-  Q

On the next deal, your spade game is contingent upon winning the trump finesse or splitting the clubs 2-2.  If both things work, you score up an overtrick.  But your postmortem has evolved toward the esoteric.  You are wondering — not whether you could make your contract, but what the chances were of winning precisely ten tricks.  In order for that to happen, you either would have to win that finesse or split the clubs, but not both.  The logical statement is "A or else B"; that operative is the "exclusive or", meaning "either A or B, but not both".  The numeric equivalent is "exactly one".

Rule #3:  The logical  (A or else B)  translates to  (a+b−2ab)

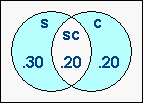This proposition is represented by the shaded area in the diagram.  As we have seen, adding the outcomes of circle s to the outcomes of circle c counts the intersection twice.  This time, however, area sc is unwanted; to delete those outcomes, it is necessary to subtract twice its value.  Let's do the numbers:  s=.50 and c=.40.  Calculating,  s+c−2sc = .5 + .4 − 2(.5 × .4) = .5, or 50%, the total of the blue areas. The likelihood of an overtrick is represented by area sc, or 20%.  The overall chance of going plus is 70%.  One can see that when solving a problem, it might be easiest simply to draw a Venn Diagram and fill in the numbers!

If no common outcomes can exist, such as in the conditions of  (diamond void in west  -or else-  diamonds 2-2), then  ab=0.

Rule #3a:  If A and B are discrete events, then the logical  (A or else B)  translates simply to  (a+b).

Putting It All Together

Now we have the tools to solve Play Problem #1 at the beginning of this article, which features contingencies for differing outstanding trump distributions in a heart game.  Since events with 3-2 trumps and those with 4-1 trumps have no common elements (they cannot simultaneously occur), they conform to Rule 3:  3-2 spades  -or else-  4-1 spades.  The entire conditions of the deal can be stated as:

(hearts 3-2  -and-  (diamond finesse  -or-  3-3 spades))
      -or else-
(hearts 4-1  -and-  (diamond finesse  -and-  3-3 spades))

In numerical terms, we have:  (h32 + (d+s−ds)) + (h41 × d × s).

As calculated in the "Mixing And with Or" section, the 3-2 trumps portion evaluates to 46%.  For 4-1 trumps,  (.28 × .5 × .36) = 5%.  Total: 51%.

Well, I declare!  If trumps split 5-0, there is no chance of taking ten tricks, and squeeze chances are slim (although they really should be included); therefore this seemingly good-looking contract — one that nearly every pair would reach — actually is only slightly odds-on.  Now you can show your partner (if he still can read your scrawls after that third margarita) why it was not so unreasonable that you went down.

Next time, play in 3NT.  That is a far better contract, and its analysis is a good way to finish this section:

On Problem #1, how often would the 9-trick game succeed against a club lead?

Well, a simple 3-2 heart split would yield nine tricks irrespective of all else; so that seems like a good place to begin the formation of our logic statement.  As distributional options other than 3-2 hearts would be discrete events subject to Rule 3, our initial statement can be:  hearts 3-2  -or else-  (other).  That 68% chance already confirms the great superiority of a notrump contract; indeed, one might be satisfied with that cursory observation and move on to the next board.  But no — you are anxious to further demonstrate your math skills, even though your partner is too far gone to appreciate them.  So the analysis continues.

What if hearts split 4-1?  Then you will have to give up a heart trick to set up the fifth card.  If clubs divide 4-4, the opponents will not have enough winners to defeat you.  However, four heart tricks brings your total only to eight; so you will need the diamond finesse as well.  This portion of our statement becomes:  hearts 4-1  -and-  clubs 4-4  -and-  diamond finesse.

What if the clubs are 5-3?  Holding up for two rounds would isolate that suit; then you could safely give up a heart trick, provided that the hand with the long clubs did not also have the long hearts.  As your contract cannot possibly succeed without a fourth heart trick, you must set up that suit; and you still would need the diamond finesse.

Expressing that contingency logically: hearts 4-1 -and-  diamond finesse   -and-  (clubs 5-3  -and-  hearts and clubs not in the same hand).

A 6-2 club division is a possibility which technically should be considered.  This exercise is complicated enough already, however, and your own eyes are beginning to blur from inebriation; so you choose to ignore that unlikely contingency just this once.

A list of known percentages is in order.  These you obtain from an index card stashed in your wallet just for this purpose:

• 3-2 hearts = .68
• 4-1 hearts = .28
• 4-4 clubs = .33
• 5-3 clubs = .47
• diamond finesse = .5

If clubs are 5-3, then one opponent has ten non-clubs to the other's eight.  So the hand with short clubs is approximately a 10-to-8 (or 5 out of 9) favorite to hold the long hearts.  Remember that this is only a rough estimate, but it is close enough for barroom work, and it yields the requisite figure:

• hearts and clubs separate = 5/9 = .56

Now, it remains to put the data into some sort of coherent format.  Let's start by reducing our statements to more concise language:

1. h32 -or else- (the rest of the formula)
2. h41 -and- c44 -and- df
3. h41 -and- df -and- (c53 -and- separate).   Let's call that last term c53s.

3-2 hearts is exclusive from 4-1 hearts; hence and 'or else' condition is appropriate between statement #1 and the others.  Statements 2 and 3 have common terms (h41 and df); so they can be evaluated inclusively, as per Rules 1 and 2.  The remaining terms, c44 and c53s, are mutually exclusive, subject to Rule 3.

The algebraic expression abc+abd can be expressed as ab(c+d), by combining the common elements.  Statements 2 and 3 can be factored in that manner to: h41 and df and (c44 or else c53s).  A reduction such as this is an important step in ensuring that the logic is valid, and it makes calculations easier.  The complete statement becomes:

hearts 3-2
     -or else-
hearts 4-1  -and-  diamond finesse  -and-  (clubs 4-4  -or else-  (clubs 5-3  -and-  suits separate))

Evaluating from the inside out as always:

• c53 and separate = .47 × .56 = .26.   This is  c53s.
• c44 or else c53s = .33 + .26 − 2(.33 × .26) = .42.   Call this  allclubs
• h41 and df and allclubs = .28 × .5 × .42 = .06

All that work for 6 percent!  Adding it to 68% for 3-2 hearts, as per Rule 3, begets a final evaluation of 74%, which is a lot better than one's chances in a heart contract.  You proudly display that revelation on your cluttered napkin, but by this time your partner has passed out.

In Conclusion

The methods presented involved mathematically straightforward situations; however, at the table other contingencies arise that are more difficult to assess for probability; In such cases, you might be called upon to make an estimate or two.

For example, as previously suggested, a long suit in an opponent's hand reduces the likelihood of a 'normal' split in any other suit.  In such situations, any bridge expert would tend to ignore the published table and take a second-round finesse with a 9-card holding, playing the preemptor for a singleton.  Similarly, if missing Q-J-10-x in the suit, then the chance of avoiding a loser will be less than the textbook value of 41%.

No mere mortal is capable of adjusting all the possible odds as the bidding and play develop; so the a-priori estimates might well be all that one has to go on.  This is not a perfect science.

Also, on the last hand discussed, the defenders were under no obligation to play that third round of clubs.  Hypothetically, at trick three an opponent, recognizing that the club suit was dead, might switch to diamonds; however, on this deal either hearts will run and there are no problems, or you will need the diamond finesse to work in any case.  So the aspect of a timely switch happens not to be an issue in this case.  In many other situations, the defenders' choices of plays — and projected likelihood of same — might need to be factored into the equation.

Addendum:   -not- (P -or- Q)

Consider the logical statement "p or q", meaning that "at least one is true".  For every statement, there is a negative, or "opposite" meaning.  The statement "not (p or q)" is the logical equivalent of  "neither is true", which is the same as (not-p and not-q).  If your contract is dependent upon the "spade split or club finesse", then clearly you will make it unless both contingencies fail to materialize — that is, no spade split and no winning club finesse.

Okay.  If a 3-2 trump split is 68%, then what is the chance of the suit not splitting favorably?  Intuitively, it is 100% − 68% = 32%.  In numerical terms, "no"  equates to (1−'yes'), and  (yes=1−no).

Rule #2n:  The logical  not (A or B)  translates to 1−(a+b−ab) = (1−a) × (1−b)

The validity of that algebraic identity is easily verified, but how can we use it?  Let's dredge up that forgettable diamond contract where you needed 3-2 trumps (68%) or a 2-2 spade split (40%).  Instead of calculating (d+s−ds), it might be easier to calculate the complement: (1−d) × (1−s).  Try it: (1 − .68) × (1 − .4) = .32 × .6 = .19, or a 19% failure rate.  Ergo, 1 − .19 = 81% success rate!  With less number-crunching.

This method comes in even handier when there are more than two variables, such as when we realized that a club finesse also was in play:  diamond split -or- spade split -or- club finesse.  Rather than using the nested procedure employed earlier, try calculating  (1−d) × (1−s) × (1−c) = .32 × .6 × .5 = .096.  Subtracting that from unity gives us a 90.4% likelihood of success — the correct value!

Evaluating Suit Potential

This is the suit in question from Problem #2 at the beginning of this article.  The contract hinges upon winning four tricks in diamonds:

♦A K   opposite   ♦10 9 4 3 2

It is necessary first to determine what outstanding card combination(s) would provide winning positions.  In this case, there are four:

1.  any 3-3 split
2.  Q J x x x x
3.  Q x J x x x
4.  J x Q x x x

#1. A 3-3 split is 36%, from tables.

#2. There are fifteen different combinations of two cards from a total of six.  Anyone familiar with the formula for such things could calculate that the "combination of 6 things taken two at a time" is equal to (6×5) ÷ (1×2) = 15,  showing that the two honors share a doubleton suit 1/15 of the time.

#3-4. With this small a sample set, one could simply itemize all the possibilities, which is easy enough:

QJ Q8 Q7 Q6 Q5 J8 J7 J6 J5 87 86 85 76 75 65

Yep, the total is fifteen.  It remains only to count the items that include an honor, learning that there are nine.  All 4-2 splits total 48%.  These are discrete entities from the hands with 3-3 splits.  Therefore, this contract will succeed whenever:

3-3 split  -or else-  4-2 split with honor(s) dropping = .36 + (.48 × 9/15)   = 65%.

A fine contract!

But what if there are 56 items?  Or 120?  Brute-force counting could become quite tedious.  Fortunately, there is Ted's Shortcut, which obviates the size of the numbers and requires only the multiplication of a couple of fractions.

A graphical representation of our experiment is useful;  let's try it on pattern #2.  Using our same Universe of six cards:  Q, J, 8, 7, 6, 5,  we will deal them to the opponents.  Envision, in the defenders' hands, slots to be filled by the cards — two on one side, four on the other, as shown:

Because it makes no theoretical difference in which order the cards are dealt, we will arbitrarily chose to deal the queen first to a random slot.  (Yes, this is valid.)  What is the likelihood that that card will go the to short (left) hand?  Clearly, it is 2 chances out of 6.  Place the queen on the doubleton side:

Next, deal the jack.  The chance of its going to the left is different now — 1 available slot out of 5 remaining.  The rest of the cards go, by default, to the other hand.  As the first two deals were mutually dependent events (Rule 1), the probability of occurrence is simply:  2/6 × 1/5 = 1/15.  How about that?

Now let's try pattern #3: Qx.  Again, deal the queen to the short hand: 2 chances in 6.  Now deal the jack to the long side:  this will occur 4 times out of 5 slots.  The overall odds are  2/6 × 4/5 = 4/15.  Dealing Jx is equally likely, for another 4/15.  The overall total for the three patterns is (1/15 + 4/15 + 4/15) = 9/15 = 3/5.

Note: Because it made no difference in the play as to which opposing hand actually held the doubleton, no further adjustment is necessary.  Anytime a suit length or card placement is hand-specific (such as requiring the doubleton to be on the left), however, the probability is reduced by half.

As suggested in the Addendum section of Part 1, it often is easier to calculate the chance of non-occurrence of an event, then subtract it from the Universe of all events — that is, 1−(non-event).

Our calculation might have been quicker had we applied that technique.  The 4-2 suit would not work for us only when one hand has QJxx.  Let us start afresh with our six-card pack.  What is the chance of dealing the queen to to the four-card holding?  Clearly 4/6, or 2/3.  Now deal the jack to that hand as well, which would occur 3 times out of 5 remaining slots.  The placement of the spot cards is immaterial; so our probability becomes: 2/3 × 3/5 = 2/5, the likelihood of failure of the suit to come home with fewer than two losers.  Therefore, 1 − 2/5 = 3/5, the chance of success.  3/5 × .48 = 29%  for favorable 4-2 combinations.  Adding that to 36% for 3-3, our total is 65%, as before.

We can advance our enquiry by altering our key suit somewhat, putting the top honors in the long hand (with a side entry to that hand):

4 3   opposite    A K 10 9 2

Still looking for four tricks, this suit could be played as before, by cashing dummy's ace and king, which we have shown is a 65% chance.  Call this Plan A.  Alternatively, we could take two finesses, Plan B.  Perhaps that is better.  We could find out by calculating the finessing options from scratch, or we could simply compare pertinent cases between the two methods.  Let's do that.

Either play works when LHO has  QJ,  Qx,  Jx,  Qxx,  Jxx,  QJx,  Jxxx,  Qxxx;  nothing works when QJxx  is offside, or when either hand holds five or more of the suit.  We can effectively eliminate those from our comparison, leaving:.

Plan A gains when RHO has QJ  or  QJx,  for then both finesses would lose.
Plan B gains when LHO has QJxx, for then no honor would drop in two rounds.

Plan A:  QJ doubleton has been calculated as 1/15 of 48%.  Using our tricky shortcut, we determine that QJx is 3/6 × 2/5 = 1/5 of 36%.   (1/15 × .48) + (1/5 × .36) = .104.  This figure must be reduced by half to 5.2%, because these suit combinations are applicable only to one side of the table. 

Plan B:  QJxx has been figured as 2/5 × .48 = .192.  This we also must divide by two, leaving 9.6%.

It appears that Plan B outscores Plan A, giving it a 69% overall rating.  In terms of total tricks, the disparity is reduced somewhat by the fact that Plan A would produce five tricks even with QJ doubleton offside.  That overtrick would accrue (1/15 × .48 / 2) = 1.6% of the time, but of course that consideration is not worth the risk of a contract.  In any case, the overall comparison is close, but taking two finesses is the mathematical winner.

The two lines of play being approximately equal in merit, this is one of those times when clues gained from the bidding or play should influence declarer's plan of attack.  The lead of a club, for example, suggests length in that suit, which reduces the likelihood of the magic QJxx in diamonds in that hand.  The more clubs on the left, the more attractive Plan A becomes; conversely, longer clubs on the right would make Plan B the standout choice.